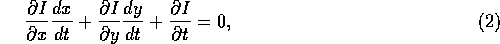
Gradient-based methods use spatial and temporal partial derivatives (or related functions; see the approach of Heeger below) to estimate image flow at every position in the image. If the image motion is not known in advance to be restricted to a small range of possible values then a multi-scale analysis must be applied (coarse to fine) so that the scale of the smoothing prior to derivative estimation is appropriate to the scale of the motion. This can result in gradient-based methods being computationally expensive. This problem is the equivalent of the correspondence problem in feature-based methods.
In [35] Enkelmann tests a gradient-based ``analytical'' method against an edge-contour-based method and a 2D-feature-point-based method, in an experiment to detect a static obstacle in front of a moving vehicle. Although all three methods appear to detect the obstacle, Enkelmann states a preference for the gradient-based method, apparently because of its reliability. However, the DROID system mentioned earlier, based on feature points, is designed for exactly this kind of situation, and has reliably found static obstacles in the path of a vehicle. Also, the gradient-based method has the weakness, which is mentioned in [35] (and which is shown in the results) that the accuracy of the outline of the obstacle is poor, due to smoothing effects. This problem would be accentuated in the case of moving obstacles.
Probably the most well known work on optic flow is [52]. Here Horn and Schunk use spatiotemporal derivatives of the evolving image brightness function to give a single equation which partially determines the optic flow; the assumption is made that the brightness of any part of the imaged world changes very slowly, so that the total derivative of the brightness is zero. When differentiated using the chain rule, this gives what is often known as the brightness change constraint equation (BCCE);
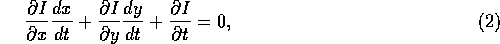
where 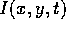 is the image brightness function. Replacing
is the image brightness function. Replacing
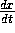 and
and 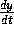 with the optic flow
with the optic flow
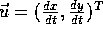 , gives the short
formulation of the BCCE;
, gives the short
formulation of the BCCE;
where 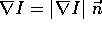 . This equation has formed the
basis of a very large proportion of research into optic flow. Horn and
Schunk note that on its own the BCCE cannot fully determine the flow;
it only gives the component of flow in the direction of the brightness
gradient. This is, of course, directly related to the aperture effect
mentioned with regard to moving edges. Thus a constraint is imposed
isotropically which forces a smooth variation in the flow across
the image. This is done in a manner very similar to that of Hildreth
described earlier, by minimizing a weighted sum of the smoothness term
(left) and the brightness change constraint expression (right);
. This equation has formed the
basis of a very large proportion of research into optic flow. Horn and
Schunk note that on its own the BCCE cannot fully determine the flow;
it only gives the component of flow in the direction of the brightness
gradient. This is, of course, directly related to the aperture effect
mentioned with regard to moving edges. Thus a constraint is imposed
isotropically which forces a smooth variation in the flow across
the image. This is done in a manner very similar to that of Hildreth
described earlier, by minimizing a weighted sum of the smoothness term
(left) and the brightness change constraint expression (right);
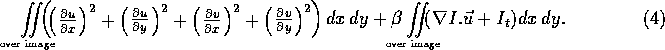
Again the weighting factor 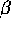 determines the relative importance
of the smoothness to the fit to the data. The optic flow is found from
this using an iterative approach; Horn and Schunk show that making one
iteration per image in a sequence of n+1 frames (carrying over the
results of the calculations to the next frame as an initial estimate)
gives better results than n iterations applied to the measurements
from just two frames.
determines the relative importance
of the smoothness to the fit to the data. The optic flow is found from
this using an iterative approach; Horn and Schunk show that making one
iteration per image in a sequence of n+1 frames (carrying over the
results of the calculations to the next frame as an initial estimate)
gives better results than n iterations applied to the measurements
from just two frames.
There are two major problems with the approach of Horn and Schunk. One is that the BCCE is only well conditioned at parts of the image which have high gradient, as can be seen in Equation 3. Thus results must be ``spread'' into those regions with low gradient if the aim of achieving flow estimates at every image position is to be achieved. The other problem is that the optic flow will be smoothed across flow discontinuities, resulting in inaccurate flow estimates. This problem was addressed by Nagel; see [72]. Here the optic flow is only smoothed in the direction perpendicular to the image brightness gradient, so that discontinuity boundaries are much better preserved. In [74], Nagel extends this ``oriented smoothness constraint'' into the temporal domain, using spatiotemporal partial derivatives of the image brightness function -- not just the spatial ones -- to determine the best ``directions'' in which to smooth.
In [72], Nagel also shows that Hildreth's work can be viewed as a special case of the ``oriented smoothness'' gradient-based approach. Similarly, in [71], Nagel discusses the relation between the flow found from using gradient-based methods and that found from using two dimensional features. He shows how the estimate of the error in the flow should vary at and around corners.
In an approach similar to gradient-based methods Heeger (see [50]) used spatiotemporal filters to find optic flow at every point in the image. The filters used here are different from those used by Buxton and Buxton (described above); they are spatiotemporal Gabor filters, created by multiplying spatiotemporal Gaussian functions with trigonometric functions to achieve band limiting and selection in the spatial and the frequency domains. Orthogonal Gabor filters are used to find the Gabor energy at 12 different orientations and at several different spatial frequencies. The strongest local velocity orientation is found, to give an estimate of image flow. The results are good, but again, there is smoothing of the flow at flow boundaries.