

Next: The Gradient-Based Approach
Up: Finding Optic Flow
Previous: Finding Optic Flow
The method of finding image displacements which is easiest to
understand is the feature-based approach. This finds features (for
example, image edges, corners, and other structures well localized in
two dimensions) and tracks these as they move from frame to frame.
This involves two stages. Firstly, the features are found in two or
more consecutive images. The act of feature extraction, if done well,
will both reduce the amount of information to be processed (and so
reduce the workload), and also go some way towards obtaining a higher
level of understanding of the scene, by its very nature of eliminating
the unimportant parts. Secondly, these features are matched between
the frames. In the simplest and commonest case, two frames are used
and two sets of features are matched to give a single set of motion
vectors. Alternatively, the features in one frame can be used as seed
points at which to use other methods (for example, gradient-based
methods -- see the following section) to find the flow.
The two stages of feature-based flow estimation each have their own
problems. The feature detection stage requires features to be located
accurately and reliably. This has proved to be a non-trivial task, and
much work has been carried out on feature detectors; see the reviews
in Sections 3 and 4. If a human is shown,
instead of the original image sequence, a sequence of the detected
features (drawn onto an empty image), then a smoothly moving set
of features should be observable, with little feature flicker. The
feature matching stage has the well known correspondence problem of
ambiguous potential matches occurring; unless image displacement is
known to be smaller than the distance between features, some method
must be found to choose between different potential matches.
Finding optic flow using edges has the advantage (over using two
dimensional features) that edge detection theory is well advanced,
compared with that of two dimensional feature detection. It has the
advantage over approaches which attempt to find flow everywhere in the
image, such as the method developed by Horn and Schunk in
[52] (see Section 1.2), that these other methods
are poorly conditioned except at image edges; thus it is sensible to
only find flow at the edges in the first place.
Most edge detection methods which have been used in the past for
finding optic flow are related to either finding maxima in the first
image derivative, see [21], or finding zero-crossings in the
Laplacian of a Gaussian of the image, see [59]. The major
problem with using edges is that unless assumptions about the nature
of the flow are made, and further processing (after the matching) is
performed, only the component of flow perpendicular to each edge
element can be found. Unfortunately, the assumptions made will
invariably lead to inaccuracies in the estimated flow, particularly at
motion boundaries, etc.
The first major work taking this approach was that of Hildreth; see
[51]. The edges are found using a Laplacian
(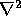 ) of a Gaussian edge detector, and the image motion is
found at these edges by using the brightness change constraint
equation (see the following section). Various additional constraints
necessary to recover the motion parallel to the edge direction are
discussed. The constraints all make the basic assumption that the
image flow is smoothly varying across the image. Thus each minimizes
some measure of flow variation. The measure chosen is the variation in
velocity along the edge contours. If this is completely minimized, the
data is largely ignored, so a balancing term is added to the
minimization equation which gives a measure of the fit of the
estimated flow to the data. Thus the following expression is
minimized;
) of a Gaussian edge detector, and the image motion is
found at these edges by using the brightness change constraint
equation (see the following section). Various additional constraints
necessary to recover the motion parallel to the edge direction are
discussed. The constraints all make the basic assumption that the
image flow is smoothly varying across the image. Thus each minimizes
some measure of flow variation. The measure chosen is the variation in
velocity along the edge contours. If this is completely minimized, the
data is largely ignored, so a balancing term is added to the
minimization equation which gives a measure of the fit of the
estimated flow to the data. Thus the following expression is
minimized;
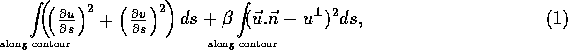
where 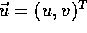 is the estimated optic flow,
is the estimated optic flow, 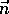 is
the unit vector perpendicular to the edge,
is
the unit vector perpendicular to the edge, 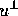 is the measured
component of flow perpendicular to the edge, s is the ``arclength''
parameter and
is the measured
component of flow perpendicular to the edge, s is the ``arclength''
parameter and 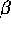 is the weighting factor which determines the
relative importance of the two terms. The first term expresses the
variation in estimated flow, and the second term expresses the quality
of the fit of the estimated flow to the measured edge displacements.
The expression is minimized using the conjugate gradient approach,
also described in [51]. The overall algorithm is
intrinsically sequential, and is fairly computationally expensive.
is the weighting factor which determines the
relative importance of the two terms. The first term expresses the
variation in estimated flow, and the second term expresses the quality
of the fit of the estimated flow to the measured edge displacements.
The expression is minimized using the conjugate gradient approach,
also described in [51]. The overall algorithm is
intrinsically sequential, and is fairly computationally expensive.
The use of edges not just in space but in space-time was introduced by
Buxton and Buxton; the theory is developed in [18], and
testing is reported in [17]. Here they use the
d'Alembertian (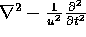 ) of a spatiotemporal Gaussian, instead of the Laplacian. The
velocity parameter u and the scale of the Gaussian filter need to be
applied at different channels to search for different motion
possibilities. Although noise suppression was claimed to be greater
than that achieved using Hildreth's approach due to the extended
dimensionality of the filter, a corresponding increase in
computational expense also resulted. In [19] this work is
extended; the negative metric is replaced with the positive one (i.e.\
) of a spatiotemporal Gaussian, instead of the Laplacian. The
velocity parameter u and the scale of the Gaussian filter need to be
applied at different channels to search for different motion
possibilities. Although noise suppression was claimed to be greater
than that achieved using Hildreth's approach due to the extended
dimensionality of the filter, a corresponding increase in
computational expense also resulted. In [19] this work is
extended; the negative metric is replaced with the positive one (i.e.\
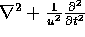 ) to
reduce noise sensitivity and removing ``curious'' cross-over effects
(mentioned in [18], but never utilized). In
[19], instead of using Hildreth's velocity smoothness
constraint, an object's motion and position parameters are estimated
directly from the measurements of the normal components of flow.
However, this ``3D solution to the aperture problem'', solved with a
least squares fit to the normal flow, assumes that the objects in
question are planar, and that the image is already segmented into
differently moving objects.
) to
reduce noise sensitivity and removing ``curious'' cross-over effects
(mentioned in [18], but never utilized). In
[19], instead of using Hildreth's velocity smoothness
constraint, an object's motion and position parameters are estimated
directly from the measurements of the normal components of flow.
However, this ``3D solution to the aperture problem'', solved with a
least squares fit to the normal flow, assumes that the objects in
question are planar, and that the image is already segmented into
differently moving objects.
In [22] Castelow et. al. use Canny edgels (edge
elements found using the Canny edge detector) to find optic flow at
edges. In this method, developed originally by Scott (see
[90]), the flow parallel to the edges is recovered by
iterative relaxation of the edgel matching surface; the edgels near
the high curvature parts of the contours can have both components of
flow found from the data, so these cues to the full flow are
propagated along the contour into less highly curved sections by
relaxation. Thus local support of optic flow is used to improve the
motion estimate iteratively. The results presented did not appear to
be as good as those shown in [51] and [19],
although the method has been successfully used by Murray et. al. to
reconstruct three dimensional objects in structure from motion work;
see
[70] and [68]. This method of finding optic flow
has also been used to track cataracts, in [45].
In [44], Gong and Brady found the full flow at points of high
curvature on zero-crossing contours using their ``curve motion
constraint equation''. The flow is then propagated along the contours
by using a wave/diffusion process. This method was developed further
by Wang et. al. in [119]. Edges are found using Canny's edge
detector, and are then segmented and grouped. ``Corners'' in the edges
are found by fitting local B-splines, and the edges at these points
are matched from one frame to the next (using a cross-correlation
method to achieve correct matches) to give the full flow. This flow is
then propagated along the edges using the wave/diffusion process. The
algorithm was implemented in parallel, and so achieved an impressive
speed compared with the original algorithm, and compared with
Hildreth's approach. The results obtained were good (for an edge-based
method), although the full flow was not always correctly estimated
along straight portions of edges. The use of high curvature parts of
edges as two dimensional features can lead to the rejection of
features which are well localized in two dimensions (and therefore
useful for recovery of optic flow) but are not placed on well defined
edges. ASSET [103,102,100] finds two
dimensional features directly from the image, and not via an
intermediate edge finding stage, and therefore avoids this problem.
Some of the ways in which edges have been used to find optic flow for
different purposes are now given.
In [30] Deriche and Faugeras track straight edges in
two dimensions using Kalman filters for each edge. The edges are found
using the Deriche filter (see [29]) and are represented by
their length, orientation and position. The resulting matched and
tracked line segments are fed into a structure from motion algorithm;
however, this approach is limited to fairly structured environments,
as it only uses straight lines.
In [12] Bolles et. al. use spatiotemporal edge filters as
developed by Buxton and Buxton (see earlier) to track features in
single raster lines over time. The tracks of features within these
raster lines create ``epipolar-plane images''; these contain
information about the three dimensional structure of the world. The
assumption is made that the images are taken in quick succession
compared with the motion of the features, so that there is no
correspondence problem. In [112] Tomasi and Kanade track
edges found using the Laplacian of a Gaussian in an approach very
similar to that of Bolles. From the tracked edges the shape of an
object is computed ``without first computing depth''. Very accurate
results are obtained, using highly constrained camera motion.
In [89] Sandini and Tistarelli use Laplacian of a Gaussian
edge contours, tracked over time by a camera moving with constrained
motion. The tracked contours are used to construct the three
dimensional structure of objects in view. In [8] Blake
and Cipolla (again, given a deliberate, constrained and known camera
motion) use the deformation of edge contours to recover surface
curvature in the world. In [36] Faugeras discusses the
problems of tracking image edges associated with non-rigid bodies. In
[24] Chen and Huang match straight line segments in stereo
sequences for object motion estimation.
Optic flow methods based on the detection of two dimensional features
(which shall be known as corners for the purpose of this discussion)
have the advantage that the full optic flow is known at every
measurement position. The (related) disadvantage is that only a sparse
set of measurements is available, compared with methods which give a
measurement at every image position. However, if the features are
found appropriately then the maximum possible number of different
optic flow measurements in the image should be recoverable, without
the degradation in flow estimate quality introduced by the various
assumptions and constraints required to recover the full flow using
other methods. Note that arguments have often been made that
gradient-based (and related) methods have their flow estimations
achieving the most well conditioned results near edges. In the same
way, flow estimates found at edges are most accurate near corners. In
the ASSET [103,102,100] system, corners are
used for finding optic flow, and image segmentation is based on this;
the segmentation results are then further refined by using
``intra-frame'' image edges. This appears to be a sensible use of the
image data, since the flow is found at those places where this can be
most accurately achieved, and remaining (instantaneous) image
information about possible object boundaries can be used to make
adjustments to the interpretation made using the flow. Another
advantage of using corners is that the early data reduction achieved
should allow computationally efficient algorithms to be developed.
Some of the published discussions on optic flow found from moving
corners and some of the ways in which this information has been
recovered and used are now described.
Much work on structure from motion has assumed that the flow field is
only recovered at relatively sparse image positions. The work has
largely consisted of theory relating how much scene information can be
given from different numbers of views of varying numbers of ``world
points''. For example, in [38] Faugeras and Maybank
show that in general the least number of point matches (found using
two viewpoints) which allows only a finite number of interpretations
of the camera positions (relative to the world) is five. With this
number of matches, there are a maximum of ten possible interpretations
of the camera's motion.
With regard to the problem of matching corners from one frame to the
next, early work was undertaken by Barnard and Thompson; see
[4]. Here the Moravec interest operator is used to find
points which are well localized in two dimensions in consecutive
images. Next, the (computationally expensive) method of iterative
relaxation of the matching surface is used to find the optimal set of
point matches. Each point in the first frame is given a probability of
matching to each point in the second; the initial probability is
inversely proportional to the sum of the squares of the difference
between the brightness of each point within a small patch centred on
the ``corner'' in the first frame and a small patch centred on the
``corner'' in the second. Then relaxation is applied to force the flow
field to vary smoothly. (This matching validation approach could be
overly restrictive in certain situations, where flow discontinuities
are important sources of information.) In [111] this
method is used to successfully detect moving objects as seen by a
moving camera; this work is discussed later.
In [23] Charnley and Blissett describe the vision system
DROID. DROID uses two dimensional features found with the Plessey
feature detector (see Section 4), and tracks these over
many frames in three dimensions using a Kalman filter for each
feature. Time-symmetric matching is performed on the basis of feature
attributes, using (where available) predicted feature positions from
the filters. The tracked features are used to construct a three
dimensional surface representing the world. The constraint is applied
that the world must contain no moving objects.
In [93] L.S. Shapiro et. al. describe a corner tracker
using the Wang corner detector (see [118]). Small inter-frame
motion is assumed. Corners are matched using correlation of small
patches. Where no matches are found, motion is predicted, using again
the correlation of small patches, in a manner very similar to the
method of Lawton (see the following paragraph). Tracking is achieved
over many frames using simple two dimensional filters which model
image velocity and (if required) image acceleration.
In [56] Lawton uses optic flow to recover world structure
assuming a static environment and translational camera motion. Image
flow is found by taking corners from one frame only, and using
correlation of small patches centred at the features with patches
placed at all possible positions in the second frame. Corners are
found by using an approach similar to that of Moravec, (see
Section 4) but are only looked for along Laplacian of
Gaussian edges. The flow is found to sub-pixel accuracy by using
inter-pixel interpolation in both frames, once the approximate
displacement has been found. Again, cross-correlation is used for
this. In [1] Adiv uses Lawton's method to find the structure
and motion of independently moving planar objects; the planar spatial
regions are later fused into multi-facet objects.
In [95] Sinclair et. al. use the motion of corners to
find three dimensional planes in the world (via projective invariants)
and also the direction of the camera's motion. Burger and Bhanu, in
[14] use the motion of ``endpoints and corners of lines as
well as centers of small closed regions'' to find the direction of
translation of the camera. Work on image segmentation using the motion
of two dimensional features includes [10],
[11], [120] and [28].
Some work has been carried out which attempts to integrate the motion
of corners and edges. In [37] Faugeras et. al. compare
recovered three dimensional structure from the motion of points and
edges theoretically and experimentally. In [107] Stephens
and Harris used edges and corners to recover the three dimensional
structure of a static environment (in a project related to the DROID
system). They integrated the tracked features with edges in an attempt
to provide wire-frame models of static objects in the world. This
integration proved difficult, and was dropped in later versions of
DROID, where edges were not used.
The details of how ASSET recovers a useful image flow field from sets
of two dimensional features are given in
[103,102,100], where some justification of
the approach taken is also given.


Next: The Gradient-Based Approach
Up: Finding Optic Flow
Previous: Finding Optic Flow
© 1997 Stephen M Smith. LaTeX2HTML conversion by Steve Smith (steve@fmrib.ox.ac.uk)
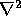 ) of a Gaussian edge detector, and the image motion is
found at these edges by using the brightness change constraint
equation (see the following section). Various additional constraints
necessary to recover the motion parallel to the edge direction are
discussed. The constraints all make the basic assumption that the
image flow is smoothly varying across the image. Thus each minimizes
some measure of flow variation. The measure chosen is the variation in
velocity along the edge contours. If this is completely minimized, the
data is largely ignored, so a balancing term is added to the
minimization equation which gives a measure of the fit of the
estimated flow to the data. Thus the following expression is
minimized;
) of a Gaussian edge detector, and the image motion is
found at these edges by using the brightness change constraint
equation (see the following section). Various additional constraints
necessary to recover the motion parallel to the edge direction are
discussed. The constraints all make the basic assumption that the
image flow is smoothly varying across the image. Thus each minimizes
some measure of flow variation. The measure chosen is the variation in
velocity along the edge contours. If this is completely minimized, the
data is largely ignored, so a balancing term is added to the
minimization equation which gives a measure of the fit of the
estimated flow to the data. Thus the following expression is
minimized;
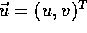 is the estimated optic flow,
is the estimated optic flow, 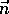 is
the unit vector perpendicular to the edge,
is
the unit vector perpendicular to the edge, 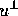 is the measured
component of flow perpendicular to the edge, s is the ``arclength''
parameter and
is the measured
component of flow perpendicular to the edge, s is the ``arclength''
parameter and 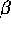 is the weighting factor which determines the
relative importance of the two terms. The first term expresses the
variation in estimated flow, and the second term expresses the quality
of the fit of the estimated flow to the measured edge displacements.
The expression is minimized using the conjugate gradient approach,
also described in [
is the weighting factor which determines the
relative importance of the two terms. The first term expresses the
variation in estimated flow, and the second term expresses the quality
of the fit of the estimated flow to the measured edge displacements.
The expression is minimized using the conjugate gradient approach,
also described in [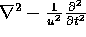 ) of a spatiotemporal Gaussian, instead of the Laplacian. The
velocity parameter u and the scale of the Gaussian filter need to be
applied at different channels to search for different motion
possibilities. Although noise suppression was claimed to be greater
than that achieved using Hildreth's approach due to the extended
dimensionality of the filter, a corresponding increase in
computational expense also resulted. In [
) of a spatiotemporal Gaussian, instead of the Laplacian. The
velocity parameter u and the scale of the Gaussian filter need to be
applied at different channels to search for different motion
possibilities. Although noise suppression was claimed to be greater
than that achieved using Hildreth's approach due to the extended
dimensionality of the filter, a corresponding increase in
computational expense also resulted. In [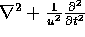 ) to
reduce noise sensitivity and removing ``curious'' cross-over effects
(mentioned in [
) to
reduce noise sensitivity and removing ``curious'' cross-over effects
(mentioned in [