The edge detection algorithm described here follows the usual method of taking an image and, using a predetermined window centred on each pixel in the image, applying a locally acting set of rules to give an edge response. This response is then processed to give as the output a set of edges.
The SUSAN edge finder has been implemented using circular masks
(sometimes known as windows or kernels) to give isotropic
responses.
Digital approximations to
circles have been used, either with constant weighting within them or
with Gaussian weighting -- this is discussed further later. The usual
radius is 3.4 pixels (giving a mask of 37 pixels), and the smallest
mask considered is the traditional three by three mask. The 37 pixel
circular mask is used in all feature detection experiments unless
otherwise stated.
The mask is placed at each point in the image and, for each point, the brightness of each pixel within the mask is compared with that of the nucleus (the centre point). Originally a simple equation determined this comparison -- see Figure 5(a);
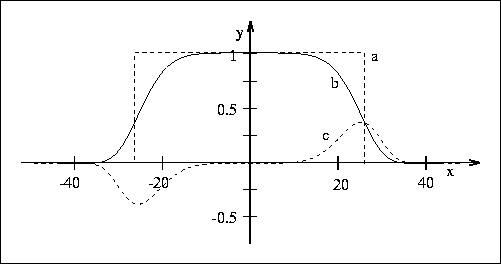
Figure 5: a) The original similarity
function (y axis, no units) versus pixel brightness difference (x
axis, in greylevels). For this example the pixel brightness difference
``threshold'' is set at 
27 greylevels. b) The more stable
function now used. c) The boundary detector B (see later text).
where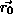 
is the position of the nucleus in the two
dimensional image, 
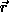is the position of any other point within
the mask,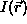 
is the brightness of any pixel, t is the
brightness difference threshold and c is the output of the
comparison.
This comparison is done for each pixel within the mask, and a running
total, n, of the outputs (c) is made;
This total n is just the number of pixels in the USAN, i.e. it gives the USAN's area. As described earlier this total is eventually minimized. The parameter t determines the minimum contrast of features which will be detected and also the maximum amount of noise which will be ignored. Further discussion later will show why performance is not dependent on any ``fine-tuning'' of the value of t.
Next, n is compared with a fixed threshold g (the ``geometric
threshold''), which is set to 
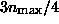, where 
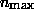is the maximum value which n can take. The initial edge response is
then created by using the following rule:
where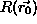 
is the initial edge response. This is clearly a
simple formulation of the SUSAN principle, i.e., the smaller the USAN
area, the larger the edge response. When non-maximum suppression has
been performed the edge enhancement is complete.
When finding edges in the absence of noise, there would be no need for
the geometric threshold at all. However, in order to give optimal
noise rejection g is set to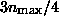 
. This value is calculated from analysis of the
expectation value of the response in the presence of noise only -- see
later. The use of g should not result in incorrect dismissal of
correct edges for the following reasons. If a step edge (of general
curvature) is considered, it can be seen that n will always be less
than (or equal to)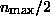 
on at
least one side of the edge. In the case of a curved edge, this will
correspond to the boundary of the region which is convex at the step
edge. Thus valid edges should not be rejected. If the edge is not an
ideal step edge but has a smoother profile then n will have even
lower minima so that there is even less danger of edges being wrongly
rejected.
The algorithm as described gives quite good results, but a much more stable and sensible equation to use for c in place of Equation 1 is
This equation is plotted in Figure 5(b). The form of Equation 4 was chosen to give a ``smoother'' version of Equation 1. This allows a pixel's brightness to vary slightly without having too large an effect on c, even if it is near the threshold position. The exact form for Equation 4, i.e., the use of the sixth power, can be shown to be the theoretical optimum; see later for analytic comparison of shapes varying from one extreme (Gaussian) to the other (square function, as originally used). This form gives a balance between good stability about the threshold and the function originally required (namely to count pixels that have similar brightness to the nucleus as ``in'' the univalue surface and to count pixels with dissimilar brightness as ``out'' of the surface). The equation is implemented as a look up table for speed. (The threshold t determines, of course, the minimum contrast of edges which will be picked up, and provides an easy way of controlling this, even automatically, if necessary.)
Computation of the edge direction is necessary for a variety of reasons. Firstly, if non-maximum suppression is to be performed the edge direction must be found. It is also necessary if the edge is to be localized to sub-pixel accuracy. Finally, applications using the final edges often use the edge direction for each edge point as well as its position and strength. In the case of most existing edge detectors, edge direction is found as part of the edge enhancement. As the SUSAN principle does not require edge direction to be found for enhancement to take place, a reliable method of finding it from the USAN has been developed. This method is now described.
The direction of an edge associated with an image point which has a non zero edge strength is found by analyzing the USAN in one of two ways, depending on the type of edge point which is being examined. For examples of the two types of edge points, see Figure 6.
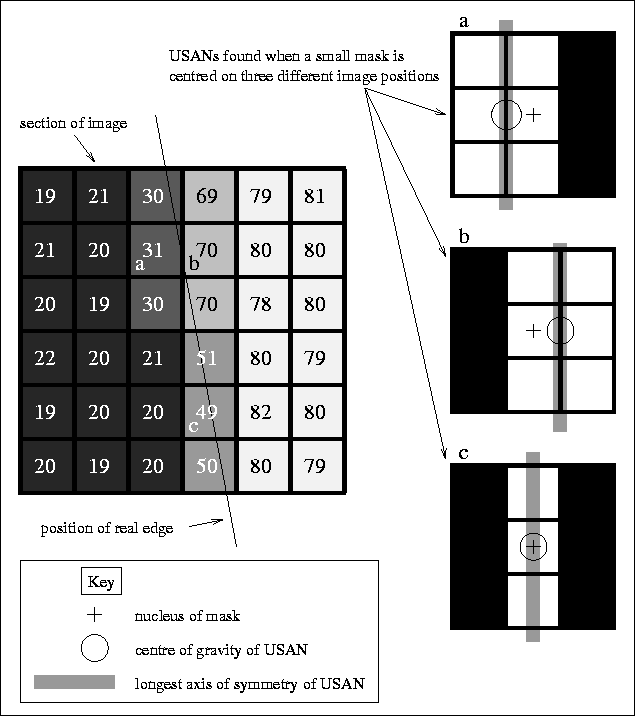
Figure 6: The two main edge types; a typical
straight edge in a section of a real image, with brightness indicated
by the numerical text as well as the shading of the pixels. The USANs
for three points of interest are shown as the white regions of a small
(3 by 3) mask. Points (a) and (b) are standard edge points, lying
definitely on one side of the edge or the other. Point (c) lies on a
band of brightness half way between the brightnesses of the two
regions generating the edge. It therefore has a differently shaped
USAN, and a centre of gravity coinciding with the nucleus.
It can be seen that points (a) and (b) have USAN shapes which would be
expected for an ideal step edge. In this case (which shall be known as
the `` inter-pixel edge case'') the vector between the centre of
gravity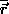 
of the USAN and the nucleus of the mask
is perpendicular to the local edge direction. The centre of gravity is
found thus;
This simple rule allows the edge direction to be found for this type of edge point.
The point shown in case (c) lies on a thin band which has a brightness roughly half way between the brightnesses of the two regions which generate the edge. This occurs when the real edge projects very close to the centre of a pixel rather than in between pixels (or when the edge is not a sharp step edge in the first place) and when the edge contrast is high. In this case, (which shall be known as the `` intra-pixel edge case'') the USAN formed is a thin line in the direction of the edge, as can be seen in Figure 6. The edge direction is thus calculated by finding the longest axis of symmetry. This is estimated by taking the sums
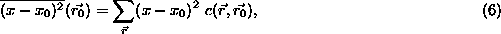
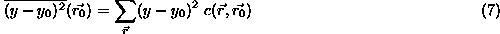
and
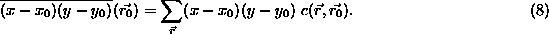
(No normalization of the sums is necessary with the second moment
calculations.) The ratio of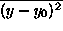 
to
is used to determine the orientation of the
edge; the sign of 
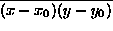is used to determine
whether a diagonal edge has positive or negative gradient. Thus in
the case of edge points like (c) the edge direction is again found in
a simple manner.
The remaining question is how to automatically determine which case fits any image point. Firstly, if the USAN area (in pixels) is smaller than the mask diameter (in pixels) then the intra-pixel edge case is assumed. Figure 6 shows clearly the logic behind this. If the USAN area is larger than this threshold, then the centre of gravity of the USAN is found, and used to calculate the edge direction according to the inter-pixel edge case. If however, the centre of gravity is found to lie less than one pixel away from the nucleus then it is likely that the intra-pixel edge case more accurately describes the situation. (This can arise for example if the intermediate brightness band is more than one pixel wide, when larger mask sizes are used.)
The edge direction can be found to varying accuracy using this method, depending on the intended application. If the final output desired is simply a binarized edge image it may be enough to simply categorize an edge element as being ``vertical'' or ``horizontal''.
An interesting point about the SUSAN edge detector is shown by the USAN areas in Figure 6. It can be simply seen that as an edge becomes blurred, the area of the USAN at the centre of the edge will decrease. Thus we have the interesting phenomenon that the response to an edge will increase as the edge is smoothed or blurred. This is most unusual for an edge detector, and is not an undesirable effect.
Finally, therefore, the edge response image is suppressed so that non-maxima (in the direction perpendicular to the edge) are prevented from being reported as edge points. Following this, the ``strength thinned'' image can be ``binary thinned''. This means that standard thinning processes can be used to ensure that the edges obey required rules about number-of-neighbour connectivity, so that remaining noise points can be removed, and so that edge points incorrectly removed by the non-maximum suppression can be replaced. A set of rules for binary thinning has been implemented (still making use of the strengths in the non-suppressed edge response image) which work well to give a good final binarized edge image. These rules are described in [63].
If the position of an edge is required to accuracy greater than that given by using whole pixels (the accuracy which would be achieved by using the theory presented so far), it may be calculated in the following way. For each edge point, the edge direction is found and the edge is thinned in a direction perpendicular to this. The remaining edge points then have a 3 point quadratic curve fit (perpendicular to the edge) to the initial edge response, and the turning point of this fit (which should be less than half a pixel's distance from the centre of the thinned edge point) is taken as the exact position of the edge.
With respect to the scale-space behaviour of the SUSAN edge detector, scale-space graphs showing edge localization against mask size (e.g., plotting a single horizontal line from the edge image against mask size, in the manner of Witkin [75]) give vertical lines. (Most edge detectors do not give scale-invariant edge positions, thus producing curves in scale-space graphs.) This is obviously a desirable feature, as it means that accuracy does not depend on mask size. This is to be expected; the minimum USAN area when approaching an edge occurs on top of the edge regardless of the mask size.
In summary then, the algorithm performs the following steps at each image pixel:
