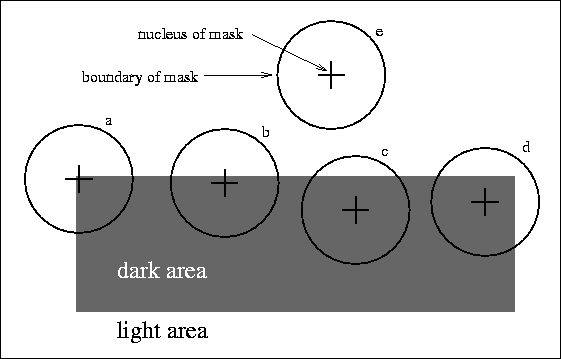
Figure 1: Four circular masks at different places on a simple image.
The SUSAN principle is now introduced, from which the research described in this paper is derived. Consider Figure 1, showing a dark rectangle on a white background. A circular mask (having a centre pixel which shall be known as the ``nucleus'') is shown at five image positions.

Figure 1: Four circular masks at different places on a simple image.
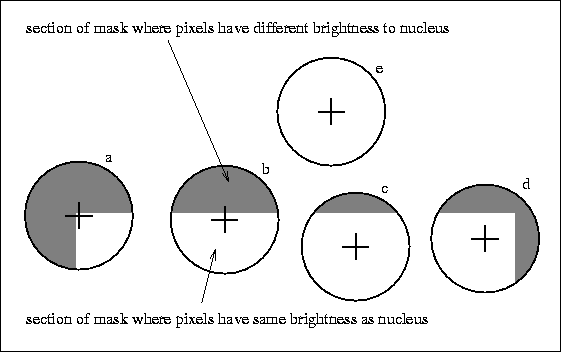
Figure 2: Four circular
masks with similarity colouring; USANs are shown as the white parts of
the masks.
If the brightness of each pixel within a mask is compared with the brightness of that mask's nucleus then an area of the mask can be defined which has the same (or similar) brightness as the nucleus. This area of the mask shall be known as the ``USAN'', an acronym standing for ``Univalue Segment Assimilating Nucleus''. In Figure 2 each mask from Figure 1 is depicted with its USAN shown in white.
This concept of each image point having associated with it a local area of similar brightness is the basis for the SUSAN principle. The local area or USAN contains much information about the structure of the image. It is effectively region finding on a small scale. From the size, centroid and second moments of the USAN two dimensional features and edges can be detected. This approach to feature detection has many differences to the well known methods, the most obvious being that no image derivatives are used and that no noise reduction is needed.
The area of an USAN conveys the most important information about the structure of the image in the region around any point in question. As can be seen from Figures 1 and 2, the USAN area is at a maximum when the nucleus lies in a flat region of the image surface, it falls to half of this maximum very near a straight edge, and falls even further when inside a corner. It is this property of the USAN's area which is used as the main determinant of the presence of edges and two dimensional features. Consider now Figure 3, where a small part of a test image has been
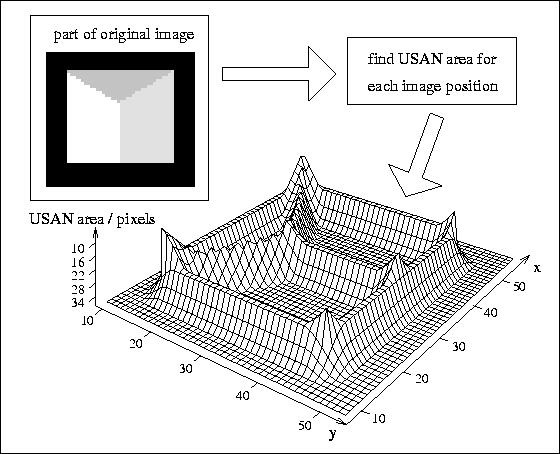
Figure 3: A
three dimensional plot of USAN area given a small part of a test
image, showing edge and corner enhancement.
processed to give USAN area as output.![]() Each point in the input image is used
as the nucleus of a small circular mask, and the associated USAN is
found. The area of the USAN is used in the three dimensional plot
shown. The USAN area falls as an edge is approached (reaching a
minimum at the exact position of the edge), and near corners it falls
further, giving local minima in USAN area at the exact positions of
image corners. Figure 4 shows a small
Each point in the input image is used
as the nucleus of a small circular mask, and the associated USAN is
found. The area of the USAN is used in the three dimensional plot
shown. The USAN area falls as an edge is approached (reaching a
minimum at the exact position of the edge), and near corners it falls
further, giving local minima in USAN area at the exact positions of
image corners. Figure 4 shows a small
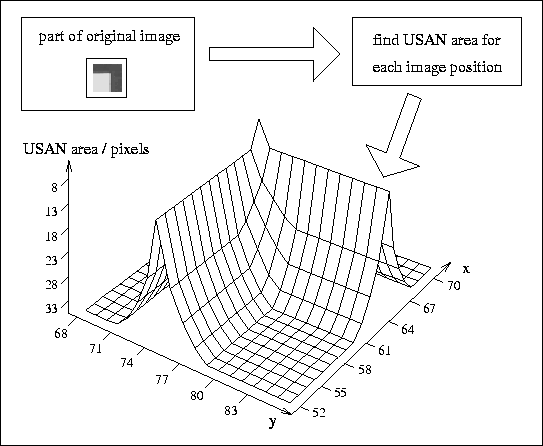
Figure 4: A three dimensional plot of USAN area given a small part of a
real noisy image, showing edge and corner enhancement.
part of a real noisy image, and the resulting output from USAN area processing. (The variation in brightness within the ``flat regions'' is of the order of 15 -- out of 256 -- greyscale levels.) Again there is edge and corner enhancement, with the noise having no visible effect on the final plot.
Consideration of the above arguments and observation of the examples and results shown in Figures 1, 2, 3 and 4 lead directly to formulation of the SUSAN principle:
An image processed to give as output inverted USAN area has edges and two dimensional features strongly enhanced, with the two dimensional features more strongly enhanced than edges.This gives rise to the acronym SUSAN (Smallest Univalue Segment Assimilating Nucleus). Mathematical analyses of the principle are given after the algorithms have been described in detail.
The fact that SUSAN edge and corner enhancement uses no image derivatives explains why the performance in the presence of noise is good. The integrating effect of the principle, together with its non-linear response, give strong noise rejection. This can be understood simply if an input signal with identically independently distributed Gaussian noise is considered. As long as the noise is small enough for the USAN function (see Figure 5) to contain each ``similar'' value, the noise is ignored. The integration of individual values in the calculation of areas further reduces the effect of noise. Another strength of the SUSAN edge detector is that the use of controlling parameters is much simpler and less arbitrary (and therefore easier to automate) than with most other edge detection algorithms.
The SUSAN noise reduction algorithm is related to the SUSAN principle in that the USAN is used to choose the best local smoothing neighbourhood.