
The SUSAN noise filtering algorithm, like some of the existing filtering techniques, preserves image structure by only smoothing over those neighbours which form part of the ``same region'' as the central pixel. Regions are commonly assumed to be constant in value; here they are only assumed to be roughly constant; sloping regions are correctly dealt with, as will be seen. The SUSAN filter works by taking an average over all of the pixels in the locality which lie in the USAN. It is obvious that this will give the maximal number of suitable neighbours with which to take an average, whilst not involving any neighbours from unrelated regions. Thus all image structure should be preserved.
The SUSAN filter is most like the gradient inverse weighted method, but instead of using the inverse gradient for each neighbour's weighting (see Equation 34), the weighting is derived from the USAN weighting, shown in Equation 4. Whereas the gradient inverse weighted method uses no ``brightness'' threshold at all, the brightness similarity equation (4) is strongly threshold dependent. This has the advantages that all neighbours within the USAN are given nearly equal weighting, and that neighbours outside the USAN are given practically zero weighting. Also, the smoothing process does not suffer when the USAN is sloping, as some variation in the USAN is allowed before the smoothing weight is significantly reduced. However, the satisfying sharp cutoff comes at the expense of needing to determine a brightness threshold. Although it is useful to be able to determine a limit to the strength of image noise (compared with the more usual determination of a lower limit to the frequency of the noise) a slightly more smoothed form for the weighting equation is used;
Thus a Gaussian in the brightness domain is used for smoothing. This means that the SUSAN filter is to the sigma filter (in the brightness and the spatial domains) what the Gaussian filter is to the box filter (in the spatial domain). The dependence of the SUSAN filter on the parameter t is not critical; it is usually not varied, but it is trivial to adjust t if ``extreme'' images are to be correctly dealt with.
Apart from the different weighting function, the other major difference between the SUSAN filter and the gradient inverse weighted method is that the sums taken over the local neighbourhood do not include the centre pixel itself. As mentioned earlier, this allows much better reduction of impulse noise than otherwise. If the resulting denominator (i.e. the USAN area) is zero (as it can be for impulse noise, due to quantization of the brightness comparison function) then the median of the eight closest neighbours is used to estimate the pixel's correct value.
Thus the complete equation used for the SUSAN filter is;
where 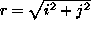 ,
,  controls the scale of the
spatial smoothing, t is the brightness threshold (which controls the
scale of the ``brightness smoothing'') and the above mentioned rule is
applied when the denominator is zero. Note that this looks quite like
the equation used for Gaussian smoothing, except that the Gaussian
function is extended into the brightness domain. The filter
clearly integrates the best aspects of the best of the existing noise
reducing filters, including edge preserving filters, described in the
previous section, and as a consequence gives very good results, as
shown below. (This integration is apparent in the theory; the
novel SUSAN filter is derived from ``first principles'', however, and
not by any attempt to actually integrate previous filters.)
controls the scale of the
spatial smoothing, t is the brightness threshold (which controls the
scale of the ``brightness smoothing'') and the above mentioned rule is
applied when the denominator is zero. Note that this looks quite like
the equation used for Gaussian smoothing, except that the Gaussian
function is extended into the brightness domain. The filter
clearly integrates the best aspects of the best of the existing noise
reducing filters, including edge preserving filters, described in the
previous section, and as a consequence gives very good results, as
shown below. (This integration is apparent in the theory; the
novel SUSAN filter is derived from ``first principles'', however, and
not by any attempt to actually integrate previous filters.)
With respect to ``deblurring'' image edges, it is clear that at a blurred edge, pixels will be pulled towards the neighbouring region to which they are closest in value. Thus, far from destroying image structure, the SUSAN filter can actually improve the image quality.
The SUSAN filter, as pointed out earlier, appears to be very similar to the approach of Saint-Marc et al. . In fact, the weighting function used in the SMCM filter has the same form as the brightness comparison part of the SUSAN filter;

where 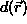 is the image gradient at
is the image gradient at 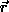 and k is a
threshold. The very important difference between this and SUSAN is
that the numerator inside the exponential is the gradient, found at
and k is a
threshold. The very important difference between this and SUSAN is
that the numerator inside the exponential is the gradient, found at
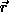 , rather than the difference in brightness between the centre
pixel and the pixel at
, rather than the difference in brightness between the centre
pixel and the pixel at 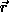 , as is the case with SUSAN. The
result of this approach with the SMCM filter is that fine structure
cannot be correctly dealt with. For example, thin lines (particularly
of two pixels width) and sharp corners are badly degraded, as pixels
on the edge of regions are wrongly excluded from calculations within
those regions. As stated earlier, the same problems exist for the
method of Perona and Malik.
, as is the case with SUSAN. The
result of this approach with the SMCM filter is that fine structure
cannot be correctly dealt with. For example, thin lines (particularly
of two pixels width) and sharp corners are badly degraded, as pixels
on the edge of regions are wrongly excluded from calculations within
those regions. As stated earlier, the same problems exist for the
method of Perona and Malik.