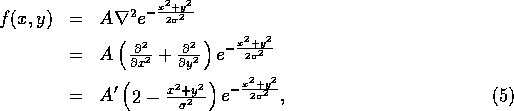
In [59] Marr and Hildreth proposed the use of zero crossings of the Laplacian of a Gaussian (LoG), that is, the use of the rotationally symmetric convolution filter,
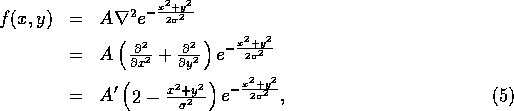
where 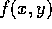 is the convolution filter, A and
is the convolution filter, A and 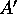 are constants
and
are constants
and 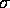 determines the spatial scale of the Gaussian. The LoG
convolution can be approximated by convolution with the difference of
two Gaussians (DoG, sometimes referred to as the ``Mexican hat'') of
appropriate scale and magnitude. The zero crossings can be tested for
spurious responses by thresholding the magnitude of the gradient of
the zero crossing. The synthesis of results found at different scales
is suggested, to enable the detection of a larger range of edge
``widths''. (See [121] for a description of a successful
approach to the synthesis of multiple scale zero crossings, and
[78] for a detailed discussion of this subject.)
determines the spatial scale of the Gaussian. The LoG
convolution can be approximated by convolution with the difference of
two Gaussians (DoG, sometimes referred to as the ``Mexican hat'') of
appropriate scale and magnitude. The zero crossings can be tested for
spurious responses by thresholding the magnitude of the gradient of
the zero crossing. The synthesis of results found at different scales
is suggested, to enable the detection of a larger range of edge
``widths''. (See [121] for a description of a successful
approach to the synthesis of multiple scale zero crossings, and
[78] for a detailed discussion of this subject.)
Contours produced using the LoG filter have the property, convenient for some purposes, of producing closed contours. However, connectivity at junctions is poor, and corners are rounded. Also, the use of non-directional derivatives means that the edge response parallel to an edge is always measured (as well as the expected response perpendicular to it), reducing the signal to noise ratio. The use of directional first and second derivatives improves on this. Finally, the LoG filter gives no indication of edge direction, which may be needed by higher level processes.