

Next: Zero Crossings of the Laplacian of a
Up: Edges
Previous: Edges
Some of the earliest methods of finding edges in images used small
convolution masks to approximate the first derivative of the image
brightness function, thus enhancing edges. Roberts (see
[85]) used masks of size two pixels by two pixels to
find orthogonal derivatives;
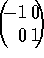 and
and
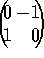 . Prewitt (see
[84]) used masks of size three pixels by three pixels in a
similar way;
. Prewitt (see
[84]) used masks of size three pixels by three pixels in a
similar way; 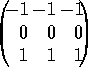 and
and 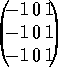 . This is preferred
to Roberts' approach because of the slightly greater amount of noise
suppression, the fact that the gradient image is not shifted by half a
pixel in both directions, and because extension to higher image
dimensions is not possible with the Roberts operator. Sobel (see
[105]) used slightly different masks to Prewitt, in that
``Gaussian averaging'' is performed in one direction, and
differentiation is performed in the other;
. This is preferred
to Roberts' approach because of the slightly greater amount of noise
suppression, the fact that the gradient image is not shifted by half a
pixel in both directions, and because extension to higher image
dimensions is not possible with the Roberts operator. Sobel (see
[105]) used slightly different masks to Prewitt, in that
``Gaussian averaging'' is performed in one direction, and
differentiation is performed in the other;
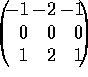 and
and 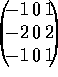 . In
[26] the Sobel filter is analyzed in terms of separable
two pixel by one pixel components, and the extension to larger filters
and more dimensions is made. The image gradient magnitude for all
three of these methods is found by taking the square root of the sum
of the squares of the outputs from the two orthogonal masks.
Likewise, the gradient direction can be found from the ratio of the
outputs of the masks.
. In
[26] the Sobel filter is analyzed in terms of separable
two pixel by one pixel components, and the extension to larger filters
and more dimensions is made. The image gradient magnitude for all
three of these methods is found by taking the square root of the sum
of the squares of the outputs from the two orthogonal masks.
Likewise, the gradient direction can be found from the ratio of the
outputs of the masks.
Other small mask operators have been suggested, such as ``compass''
operators, which have more than two masks, oriented in several
directions. In [48] the responses to gradient magnitude
of several small gradient masks are analyzed. It is shown that the
choice of mask should depend on the type of image noise present. It is
also shown that the isotropy of response does not depend much on the
choice of mask.


Next: Zero Crossings of the Laplacian of a
Up: Edges
Previous: Edges
© 1997 Stephen M Smith. LaTeX2HTML conversion by Steve Smith (steve@fmrib.ox.ac.uk)
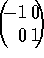 and
and
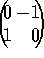 . Prewitt (see
[84]) used masks of size three pixels by three pixels in a
similar way;
. Prewitt (see
[84]) used masks of size three pixels by three pixels in a
similar way; 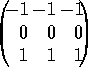 and
and 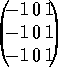 . This is preferred
to Roberts' approach because of the slightly greater amount of noise
suppression, the fact that the gradient image is not shifted by half a
pixel in both directions, and because extension to higher image
dimensions is not possible with the Roberts operator. Sobel (see
[105]) used slightly different masks to Prewitt, in that
``Gaussian averaging'' is performed in one direction, and
differentiation is performed in the other;
. This is preferred
to Roberts' approach because of the slightly greater amount of noise
suppression, the fact that the gradient image is not shifted by half a
pixel in both directions, and because extension to higher image
dimensions is not possible with the Roberts operator. Sobel (see
[105]) used slightly different masks to Prewitt, in that
``Gaussian averaging'' is performed in one direction, and
differentiation is performed in the other;
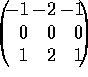 and
and 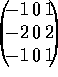 . In
[26] the Sobel filter is analyzed in terms of separable
two pixel by one pixel components, and the extension to larger filters
and more dimensions is made. The image gradient magnitude for all
three of these methods is found by taking the square root of the sum
of the squares of the outputs from the two orthogonal masks.
Likewise, the gradient direction can be found from the ratio of the
outputs of the masks.
. In
[26] the Sobel filter is analyzed in terms of separable
two pixel by one pixel components, and the extension to larger filters
and more dimensions is made. The image gradient magnitude for all
three of these methods is found by taking the square root of the sum
of the squares of the outputs from the two orthogonal masks.
Likewise, the gradient direction can be found from the ratio of the
outputs of the masks.