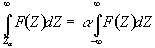 . (6.23)
. (6.23)
The statistical analysis techniques discussed in the last section all result in a statistical parametric map (SPM), where each pixel in the image is assigned a value based on the likelihood that the null hypothesis is false. However for the localisation and comparison of brain function, what is required is an image which only highlights those pixels which can confidently be labelled as active. This is done by thresholding the statistical parametric map.
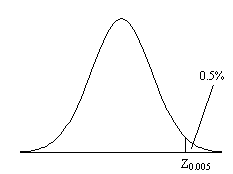
Before approaching the problem of the significance of whole images, it is necessary to consider the question of the confidence that can be placed in the result of a single t-test, correlation or ANOVA. Such levels come from an understanding of the distribution, under the null hypothesis, of the statistic being considered. If for example a statistic had a normal distribution, as shown in Figure 6.16, a critical value Za can be defined such that
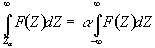 . (6.23)
. (6.23)

This means that if the value of Z obtained in the statistical calculation is greater than Z0.005, we can be 99.5% confident the null hypothesis is false. The number 0.005 in such a case is said to be the p-value for that particular test. Such values are tabulated in standard statistical texts, or can be obtained directly from expressions for the distributions themselves.
The distribution for a correlation coefficient is dependent on the number of degrees of freedom in the time course being analysed. For a time course of n independent time points, there are n-2 degrees of freedom. The question of whether time points from an fMRI experiment are independent is addressed later in this section. The correlation coefficient, r, can be transformed so that it has a Z distribution (that is a Gaussian distribution with zero mean and unit variance), by applying the Fisher Z transform
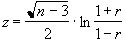 . (6.24)
. (6.24)
This transform may therefore be applied to the SPM of correlation coefficients, yielding an SPM of z scores.
The theory of Gaussian random fields (as described later, in section 6.4.3), applies to images of z scores. Therefore it is necessary to transform the t and f scores to z scores as well. This is done by calculating the area under the distribution (p value) between t and infinity (or f and infinity), and choosing an appropriate value of z such that the area under the Z distribution between z and infinity is the same.
P-values for the t-statistic are related to the incomplete beta function
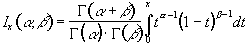 (6.25)
(6.25)
such that
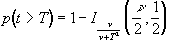 (6.26)
(6.26)where n is the number of degrees of freedom, which is equal to the number of data points that were used to construct the statistic minus one.
Similarly p-values for the f-statistic can be derived from
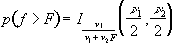 (6.27)
(6.27)
where n1 is the number of points per cycles minus one and n2 is the total number of points minus the number of points per cycle (n1=k-1, n2=k(n-1)).
The transforms are carried out using pre defined functions in the package MATLAB[20], to calculate the incomplete beta function and the inverse error function.
All the statistical tests assume that the data points are independent samples of the underlying population. This however may not be the case, since the effect of the haemodynamic response function, and any temporal smoothing that is applied to the data, means that adjacent time points are no longer independent. This has an effect on the effective number of degrees of freedom in the sample.
A detailed analysis of this problem is given in by Friston et. al.[21-23], but a more intuitive explanation of his result is given here.
Consider a series of n independent observations of a population of mean m.
The variance of the population is given by
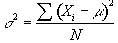 (6.28)
(6.28)
which is best estimated by the sample variance
 . (6.29)
. (6.29)
The denominator in this expression is the number of degrees of freedom of the sample, and is one less than the number of observations, since only n-1 points are needed to describe the sample, the 'last' point being determined by the mean.
Now if the above data set is smoothed with a three point running filter such that
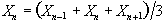 .
.

The sum of the square deviations from the mean of the data is now (on average) three times less than that of the unsmoothed data. This means that the population variance is now best approximated by
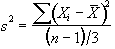 (6.30)
(6.30)
and implying that the smoothed data set has (n-1)/3 degrees of freedom. In the case of the pre-processing described above, the smoothing filter is a Gaussian kernel, as opposed to the three point running average.
In this case it is necessary to evaluate the effect of neighbouring data points on any one point, and so the reduction in the number of degrees of freedom is given by the area under the Gaussian kernel. The number of degrees of freedom in the sample variance for a data set of n sample points, smoothed with a Gaussian of standard deviation s is therefore
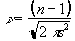 . (6.31)
. (6.31)
Simulations of the effect of smoothing data before carrying out an analysis of variance calculation show that such a degrees of freedom reduction does not hold in this case. Temporal smoothing of the data is unlikely to improve the ability of the ANOVA test to detect activations, and is therefore best not applied, however high pass filtering is likely to improve the test and should still be used.
A summary of the number of degrees of freedom for the tests described earlier is given below.
All the reasoning so far in this section is to do with the p values concerned with one statistical test. That is to say, for one individual pixel, we can be confident to a certain value of p, that its time course is correlated to the stimulus. When we form an image from the results of such statistical tests, it is necessary to consider how confident we are that none of the pixel labelled as 'active', are in fact due to random fluctuations. Take for example the SPM shown in Figure 6.17.

Here a pixel is shaded if a statistical test shows that the pixel is active, with a p value greater than 0.1. Since there are 100 pixels in the image, it is probable that 10 pixels will, by chance, be falsely labelled as active. The p value for such an image would therefore be 1.0, that is to say that we are certain that at least one of the pixels is falsely labelled. This situation is called the multiple comparisons problem, and is well studied in statistics[24].
If all the pixels can be considered to be independent, then a Bonferroni correction can be applied. This states that for an image of N pixels, the overall probability of any false positive result is P, if the individual pixel false positive probability is P/N. However with thousands of pixels in an image, such a technique is very stringent, and the risk of falsely rejecting true activations is very high. There is also the question of whether each pixel in the image can truly be regarded as independent. The point spread function of the imaging process means that adjacent pixels cannot vary independently, and this situation is worse if additional smoothing is applied.
Such problems were first addressed in PET data analysis, and the results carried over to fMRI. The theory of Gaussian random fields[25], was developed for the analysis of functional imaging data by Friston et. al.[26] and an overview of their important results is presented here.
For a completely random, D-dimensional, z-statistical parametric map consisting of S pixels, the expected number of pixels that are greater than a particular z score threshold, u, is given by
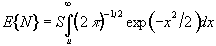 . (6.32)
. (6.32)
This is the area under the Gaussian distribution as shown in Figure 6.16. The theory attempts to estimate the number of discrete regions there will be above this threshold. Take for example the SPM shown in Figure 6.18a. This is formed from a simulated data set with completely independent pixels. Those pixels with z-scores above a certain threshold are shown in white with those lower in black. The same data set, spatially smoothed before analysis is shown in Figure 6.18b. The number of white pixels in each SPM is about the same, but the number of discrete regions of white pixels is much less in the smooth case.
(a) (b)
(b)
The expected number of regions appearing above u is estimated by
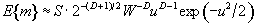 (6.33)
(6.33)
where W is a measure of the 'smoothness', or resolution of the map. This is obtained by measuring the variance of the first derivative of the SPM along each of the dimensions
 . (6.34)
. (6.34)
The average size of a region is thus given by
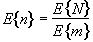 . (6.35)
. (6.35)
Once these quantities have been estimated, the question is, what is the probability that a region (of activation) above a certain threshold u of size k pixels, could occur purely by chance. If k is of the order of E{n} then this probability is quite high, but if k»E{n} then the probability reduces. The form of this probability distribution is taken as
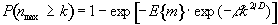 (6.36)
(6.36)
where nmax is the size of the maximum region above u, in a random SPM, and
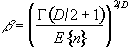 . (6.37)
. (6.37)
Thus for a given SPM the smoothness parameter W can be calculated, and only those regions above a chosen value of u that are of size greater than a chosen k are shown, the p value for the activation image can be calculated using equations 6.32 - 6.37.
Having thresholded the SPM to display only those 'active' regions, these regions must be superimposed on background images to enable anatomical localisation. If the EPI images that the fMRI data comes from are of suitable quality, then these can be used as the base images. Better contrast may come from some inversion recovery images (see Section 2.4.1) showing only white matter, or grey matter. This is the practice used for the images shown in Chapter 7, and has the advantage that any distortions in the images will be the same for both activation and background, and no image realignment is needed. Higher resolution EPI images with equal distortion can be obtained using interleaved EPI as discussed in Chapter 5. To obtain really high quality base images it is necessary to use a 2DFT technique, however the distortions in such an image will be much less than the EPI functional images, and some form of alignment and 'warping' is required in this case.
The subject of comparing results from a number of different experiments, either on the same person at different times, or between different people, raises many issues, only a few of which are covered here.
Qualitative comparisons between subjects can be made by a good radiologist, familiar with EPI images, however in order to quantify differences it is necessary to try and 'normalise' the differences between the brains of the subjects. This has traditionally been done in functional imaging by using the atlas of Talairach and Tournoux[27], based on slices from the brain of a single person. It uses a proportional grid system based on the location of two anatomical landmarks, the Anterior Commissure (AC) and the Posterior Commissure (PC). Having identified the locations of the AC, PC, and the superior, inferior, left, right, anterior and posterior edges of the brain, these co-ordinates are rotated until the line joining the AC and PC is along the x axis, and the line joining the left and right markers is parallel to the z axis (Figure 6.19).
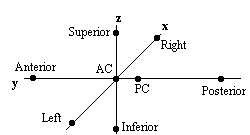
The same rotations are performed on any 'activation' region, and the co-ordinates are then scaled to give a distance in millimetres from the AC in each dimension, such that
These readings can then be looked up in the atlas to determine the location of the activation. Alternatively the whole image set can be similarly transformed to give a Talairach normalised set of images.
The main drawback of this technique is that it is based only on the brain of one person, and since gyri and sulci vary significantly between people, the reliability of using such an atlas is questionable. It is also questionable as to whether the proportional grid system is reliable enough to transform the images. As an alternative it is possible to warp the image until it fits the Talairach atlas brain[28]. If warping is used, then there are more appropriate templates available, which are based on MRI scans of a number of subjects. These templates attach probabilities to the spatial distribution of the anatomy[29], and are more reliable than a single subject template.
Even if the brains of several subjects are in some way normalised, there are questions as to how significant are differences in the magnitude of the signal change from one subject to another. A large amount of subject movement during the scanning will reduce the statistical likelihood of detecting activations. This could mean that activation which is present, but not detectable due to poor signal to noise, could be interpreted as no activation at all. Such problems have no easy solution, and more work is required in this area.
Consideration of these problems for a specific experiment is given in Chapter 7.
Software was written which allowed the user to interactively change the values of u and k, and to look at the effect that this has on the activation image and its p-value. The graphical user interface (shown in Figure 6.20) is written in the scripting language 'perl'[30], which calls other 'C' programs to carry out most of the calculations and data manipulation.
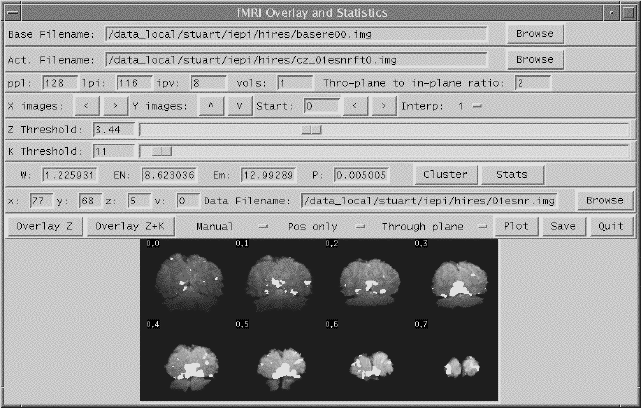
SPMs of z-scores, stored as floats, are read in and thresholded at a z-score specified by a slider. These are displayed as white pixels, above a greyscale base image. The user can choose an appropriate cluster size threshold by either changing the slider or clicking on one of the regions with the mouse, and asking for the calculation of the size of that cluster. The activation image, with both thresholds applied can be displayed, and the p-value for such a combination calculated. It is necessary to change both thresholds interactively to find the optimum activation image for a given p-value, however results from Friston[31] suggest that wide signals are best detected using low z-thresholds and sharp signals with high z-thresholds.
The time course plots for any selected region can be displayed, with the 'plot' option. Any file can be chosen to take the plot intensities from, allowing the whole experiment time course, the average for one cycle, or Fourier components for the region to be displayed, provided that an image file containing such data exists.
Having chosen an appropriate set of thresholds, the images can be saved for display. The 'save' option allows any image file to be overlaid upon the base file, masked by the thresholded SPM. The base images are scaled between 0 and 20,000, and the 'active' regions scaled between 20,000 and 32,000, which allows an appropriate image viewing package to display the base images in greyscale and the activation in colour-scale. If the statistic used is also a good indicator of the magnitude of activation signal change, for example the t-statistic for the difference between 'rest' and activity, then it is appropriate to display in colour-scale the pixel values from the SPM. However for statistics such as the correlation coefficient, the values do not represent the amount of signal change. In these cases it is more appropriate to display values from a percentage change image in colour, masked by the thresholded SPM. In order to appropriately identify the anatomical location of the activation, it is sometimes desirable to see the brain structure that underlies the activation. In this case it is appropriate to use the base images as the source of the values for the activation regions. This means that the effect can be created where the background image is in greyscale, and the active regions are 'shaded' in red-scale. Examples of overlaying SPMs, regressions and base sets are shown in Figure 6.21.
| (a) |  |
| (b) |  |
| (c) |  |
The software can also calculate the Talairach co-ordinates of any region, provided that the appropriate landmarks can be identified (or deduced) from the images. Having entered the co-ordinates of the landmarks, and chosen a region of interest, the co-ordinate system is rotated and proportionated, to give the distances in millimetres from the Anterior Commissure, of the centre of mass of that region in Talairach space.
The user instructions for the software is included as Appendix C.