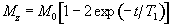 .
.
Unlike many other medical imaging modalities, the contrast in an MR image is strongly dependent upon the way the image is acquired. By adding r.f. or gradient pulses, and by careful choice of timings, it is possible to highlight different components in the object being imaged. In the sequence descriptions that follow it is assumed that the imaging method used is EPI, however identical or similar methods can be used with the other MR imaging techniques outlined above.
The basis of contrast is the spin density throughout the object. If there are no spins present in a region it is not possible to get an NMR signal at all. Proton spin densities depend on water content, typical values of which are given in Table 2.2 for various human tissues [23]. The low proton spin density of bone makes MRI a less suitable choice for skeletal imaging than X-ray shadowgraphs or X-ray CT. Since there is such a small difference in proton spin density between most other tissues in the body, other suitable contrast mechanisms must be employed. These are generally based on the variation in the values of T1 and T2 for different tissues.
| Tissue | % Water Content |
| Grey Matter | 70.6 |
| White Matter | 84.3 |
| Heart | 80.0 |
| Blood | 93.0 |
| Bone | 12.2 |
When describing the effect of the two relaxation times on image contrast, it is important to distinguish between relaxation time maps, and relaxation time weighted images. In the former the pixel intensities in the image have a direct correspondence to the value of the relaxation time, whilst in the latter the image is a proton density image which has been weighted by the action of the relaxation.
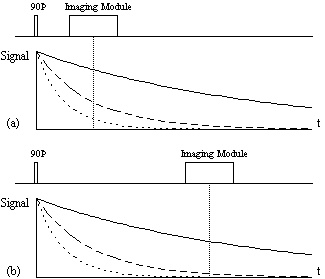
The spin-lattice relaxation time T1, is a measure of the time for the longitudinal magnetisation to recover. A proton density image can be weighted by applying an r.f. pulse which saturates the longitudinal magnetisation prior to imaging. Spins that have recovered quickly will have greater available z-magnetisation prior to imaging than those which recover slowly. This effect is apparent if the same slice, or set of slices, are imaged rapidly, because the excitation pulse of the previously imaged slice affects the magnetisation available for the current slice. More commonly however, if T1 maps, or T1 weighted images are required then the imaging module is preceded by a 180 degree pulse (Figure 2.20). The 180 degree pulse will invert the longitudinal magnetisation, whilst not producing any transverse magnetisation. The recovery of the longitudinal magnetisation is governed by the Bloch equation for Mz, which has the solution
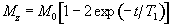 .
.
(2.60)
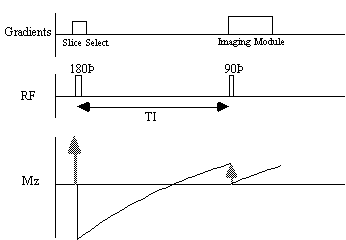
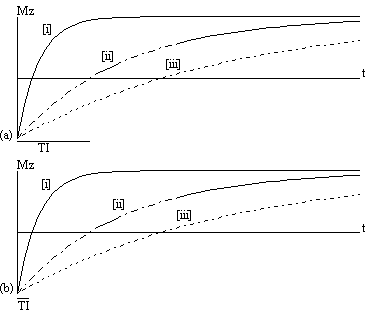
The magnetisation is allowed to recover for a time TI, after which it is imaged using a 90 degree pulse, and usual imaging gradients. The amount of signal available will depend on the rate of recovery of Mz. If, as in Figure 2.21, the sample has spins with several different relaxation times, it is possible to choose TI such that the signal from spins with one recovery curve is nulled completely, whilst giving a good contrast between spins with other recovery curves. Figure 2.22 shows some examples of T1 weighted images. In order to calculate the values of T1, to create a T1 map, it is necessary to obtain a number of points along the magnetisation recovery curve, and then fit the points to the equation 2.60. The most straightforward way to do this is to repeat the inversion recovery sequence for a number of values of TI, but there are techniques which acquire all the data in a single recovery curve [24, 25].
(a) 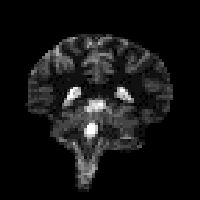 (b)
(b) 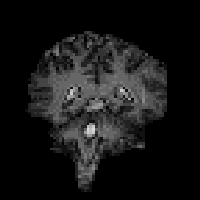
The problem with measuring T2 with a sequence which relies on a gradient echo (as EPI does) is that there is a confounding effect which erodes the transverse magnetisation in the same way that spin-spin relaxation does, which is that of field inhomogeneities. If the spins in a single voxel do not experience exactly the same field, then the coherence of their magnetisation will be reduced, an effect which increases with time. The combined effect of spin-spin relaxation and an inhomogeneous field on transverse magnetisation is characterised by another time constant T2*, and the decay of the signal is governed by the equation
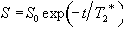
(2.61)
In fact T2* weighted images are desirable for functional MRI applications, as is explained in the next chapter. To change the T2* weighting of an image, it is only necessary to change the time between the excitation pulse and the imaging gradients. The longer the delay, the greater the T2* weighting, as shown in Figure 2.23. Examples of T2* weighted images are shown in Figure 2.24. T2* maps can be obtained by taking several images with different delays, and fitting to equation 2.61. A technique for obtaining T2* maps from a single FID is explained in Chapter 4.
(a) 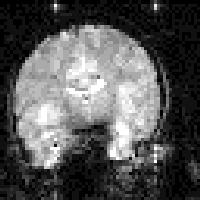 (b)
(b)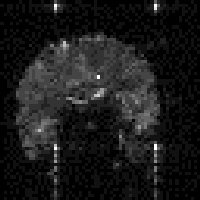
It is possible to obtain the real value of T2 by refocusing the effect of field inhomogeneity on the transverse magnetisation using a spin-echo. A spin-echo is formed by applying a 180 degree pulse, a time t after the excitation pulse. This has the effect of refocusing the signal at time 2t (Figures 2.25, 2.26).
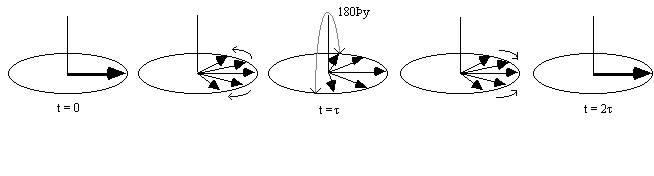
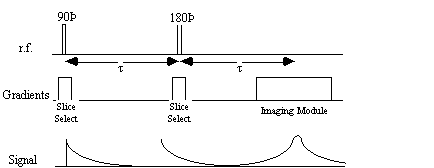
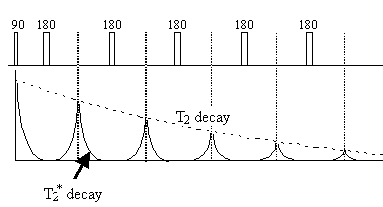
Since the spin-spin relaxation is not refocused in the spin echo, the contrast in the image is dependent on T2 and not T2*, with contrast being dependent on the delay between the excitation pulse and the imaging module. Again T2 maps can be made from images with different delay times (called the echo time, TE), by fitting to the T2 decay equation which is similar to equation 2.61. Multiple echoes can be formed by using a series of 180 degrees pulses as shown in Figure 2.27.
In order to improve the contrast of images, it is common to use some form of contrast agent. The most common of these in MRI is gadolinium, which is a paramagnetic ion, and reduces the spin-lattice relaxation time (T1) considerably.
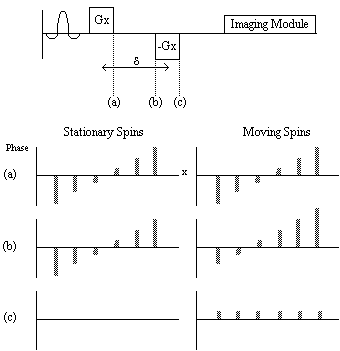
One of the usual assumptions about imaging using magnetic resonance is that the spins are stationary throughout the imaging process. This of course may not be true, for example if blood vessels are in the region being imaged. Take for example the situation of imaging a plane through which a number of blood vessels flow. A slice is selected and all the spins in that slice are excited, however in the time before imaging, spins in the blood have flown out of the slice and unexcited spins have flown in. This means that there may be no signal from the blood vessels.
In order to measure the rate of flow, some kind of phase encoding that is flow sensitive can be applied. This is done by applying a magnetic field gradient along the direction in which flow is to be measured. A large gradient dephases the spins depending on their position along the gradient. This gradient is then reversed, which will completely rephase any stationary spins. Spins that have moved however will not be completely rephased (Figure 2.28). If the flow is coherent within a voxel, when the spins are imaged the phase difference can be calculated, and by varying the time between the forward and reverse gradients the flow can be calculated. Diffusion is measured in a similar way, but since the motion of the spins within the voxel is not coherent, the effect of diffusion is simply to diminish the signal.