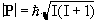
The quantum mechanical description of atomic nuclei, as described by Dirac in 1930, predicted the property of spin angular momentum. In fact the property of electron spin was observed six years earlier by Stern and Gerlach [7], who passed a beam of neutral atoms through a non-uniform magnetic field, and observed the effect of half-integral angular momentum, that could not be explained by the previously accepted Bohr model.
This spin angular momentum is characterised by the spin quantum number I, such that the total spin angular momentum is Ih. The value of I is an intrinsic property of the nucleus, examples of which are given in Table 2.1.
| Nucleus | Spin Quantum Number I |
| 1H | 1/2 |
| 2H | 1 |
| 12C | 0 |
| 13C | 1/2 |
| 19F | 1/2 |
| 31P | 1/2 |
To exhibit the property of magnetic resonance the nucleus must have a non-zero value of I. As far as medical applications are concerned, the proton (1H) is the nucleus of most interest, because of its high natural abundance. However, other nuclei have been studied, most noticeably 13C whose low natural abundance relative to 12C makes it suitable for tracer studies.
The magnitude of the spin angular momentum is given by
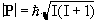
(2.1)
but since P is a vector, its orientation must be taken into account. In a magnetic field, applied along the z axis, the possible values of the z-components of the angular momentum are given by
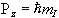
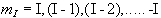 .
.(2.2)
So for the proton, with spin 1/2, there are two possible values
for 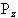 , that is
, that is 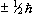 .
The eigenfunction describing
the spin state of the proton nucleus can be written as
.
The eigenfunction describing
the spin state of the proton nucleus can be written as 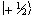 or
or 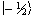 ,
and since in quantum mechanics every physical
observable has an associated operator, we can write an eigenvalue
equation to describe the observation of the spin state as
,
and since in quantum mechanics every physical
observable has an associated operator, we can write an eigenvalue
equation to describe the observation of the spin state as
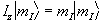
(2.3)
where 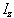 is the operator
describing measurement of the angular momentum along the z axis.
There are similar operators for measuring the angular momentum along
the x and y axes, so we have a range of eigenvalue equations for a
spin 1/2 system as follows:
is the operator
describing measurement of the angular momentum along the z axis.
There are similar operators for measuring the angular momentum along
the x and y axes, so we have a range of eigenvalue equations for a
spin 1/2 system as follows:
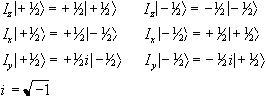
(2.4)
To measure the energy of the spin system it is necessary to construct a Hamiltonian operator. The form of the Hamiltonian can be derived from classical electromagnetism for the energy of a magnetic moment placed in a magnetic field.
Nuclei have a magnetic moment, m, which is proportional to the angular momentum,
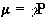
(2.5)
Nuclei with the constant of proportionality, g, being called the magnetogyric ratio. The magnetogyric ratio is a property of the particular nucleus, and has a value of 2.675 x 10 8 rad/s/T for protons. When this magnetic moment is placed in a magnetic field, B, it has energy
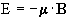
(2.6)
and so by combining equations 2.5 and 2.6 a Hamiltonian can be defined as
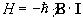 .
.
(2.7)
Since by definition the B field is applied parallel to the z-axis the Hamiltonian becomes
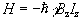
(2.8)
and is known as the Zeeman Hamiltonian. Now using the Schrödinger equation, the energy of the eigenstate is found.
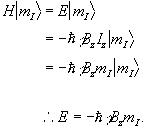
(2.9)
So for a proton with 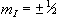 , a transition between
the two states represents a change in energy
, a transition between
the two states represents a change in energy
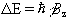
(2.10)
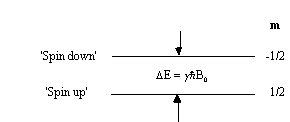
This is called the Zeeman splitting, and is shown as an energy level diagram in Figure 2.1. These two states are given a variety of labels, but most commonly referred to as 'spin up', and 'spin down', with the spin-down state having a higher energy than the spin-up state. Transitions between the two states can be induced by absorption or emission of a photon of frequency n 0, such that
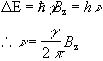
(2.11)
Expressing the frequency in angular terms gives the Larmor equation which underpins the whole of NMR
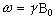
(2.12)
the characteristic frequency, w, being the Larmor frequency. The magnetic field, labelled B0, is still assumed to be applied along the z axis, and is now subscripted with a '0' to distinguish it from the applied radio frequency field which will be introduced later.
This description of the quantum mechanical behaviour of an atomic nucleus leads to the way NMR is performed. Transitions between the two energy states, spin-up and spin-down, can occur by absorption or emission of electromagnetic radiation of frequency given by the Larmor equation. This frequency depends, for a given species of nuclei, purely on the applied magnetic field. It is the strength of the field experienced by the nucleus that enables structure to be determined in spectroscopy experiments, and position to be found in imaging experiments.
In a real system there is not just one nucleus in isolation, but many nuclei all of which could occupy a particular spin state. This means that the theory must be extended to consider an ensemble of spins.
To do this a single eigenstate Y, which is a linear combination of the possible spin states for a single nucleus is defined
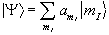
(2.13)
When making a measurement on such a system, the expectation value of the operation on this superposition of states is
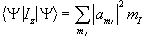
(2.14)
where the value 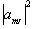 represents the probability
of finding a single nucleus in the state mI. So for
the case of a proton, with two spin states
represents the probability
of finding a single nucleus in the state mI. So for
the case of a proton, with two spin states
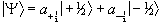
(2.15)
The ratio of the populations of the two energy states from Boltzman statistics is
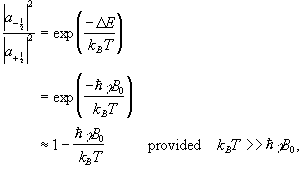
(2.16)
so the difference between the number of spins in the spin-up state and the spin-down state is
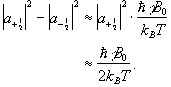
(2.17)
If we now assume that all the 'spin up' nuclei have a
magnetic moment of 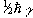 and the 'spin down'
nuclei have a magnetic moment of -
and the 'spin down'
nuclei have a magnetic moment of -![]() , then we can write the bulk magnetisation of the ensemble
as
, then we can write the bulk magnetisation of the ensemble
as
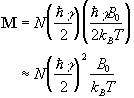
(2.18)
where N is the number of spins in the ensemble. Being able to treat the behaviour of all the spins in the system in terms of magnetisation allows a transfer from a quantum mechanical to a classical description of NMR. The advantage of the classical description is that it gives a simpler picture of the NMR experiment.
If the spin magnetisation vector M is placed in a magnetic field B, M will experience a torque. The equation of motion for M can be written
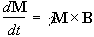 .
.
(2.19)
If B is a static (time-independent) field along the z axis
such that 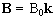 then equation 2.19 becomes
then equation 2.19 becomes
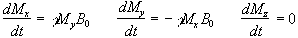
(2.20)
which has solutions
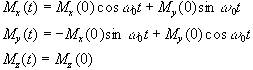
(2.21)
where 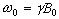 . These equations describe the
precession of the magnetisation vector about the z axis as shown in
Figure 2.2. The angular frequency of the precession is identical to
the Larmor frequency derived in the quantum mechanical description
above (equation 2.12), showing how the classical and quantum
mechanical pictures coincide.
. These equations describe the
precession of the magnetisation vector about the z axis as shown in
Figure 2.2. The angular frequency of the precession is identical to
the Larmor frequency derived in the quantum mechanical description
above (equation 2.12), showing how the classical and quantum
mechanical pictures coincide.
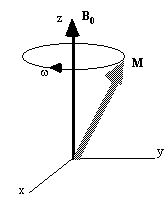
Now, as well as the static B0 field applied along z, consider a time varying field B1, applied perpendicularly to B0 and oscillating at w0. If only the circularly polarised component of B1 rotating in the same direction as the precessing magnetisation vector is considered
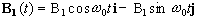
(2.22)
which when put into equation 2.19 yields
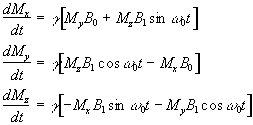
(2.23)
If a starting condition M(0)=M0k is defined, then the solutions for M are
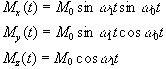
(2.24)
where 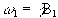 .
.
This implies that by applying an oscillating magnetic field of frequency w0, the magnetisation simultaneously precesses about B0 at w 0 and B1 at w 1, as shown in Figure 2.3a.
At this point it is appropriate to introduce a new frame of reference for viewing the evolution of the magnetisation vector, the rotating frame, which rotates about the z-axis at frequency w 0. If in the rotating frame an axis system (x',y',z) is defined then equation 2.19 can be written
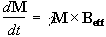
(2.25)
where
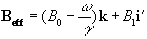
(2.26)
and (i',j',k) are unit vectors in the (x',y',z)
directions. The result of solving
these two equations is a magnetisation vector which precesses about
Beff, as
shown in Figure 2.3b. If  and M precesses about the x' axis shown in Figure 2.3c.
Applying the B1
field has the effect of rotating the magnetisation
vector about the x'-axis at an angular frequency
w1=
g
B1.
and M precesses about the x' axis shown in Figure 2.3c.
Applying the B1
field has the effect of rotating the magnetisation
vector about the x'-axis at an angular frequency
w1=
g
B1.
(a)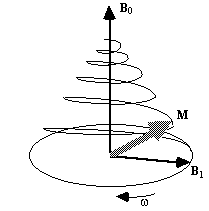
(b)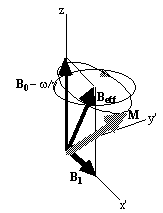
(c)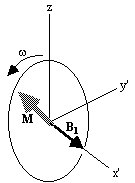
The most common way to carry out an NMR
experiment is to apply a short burst of resonant r.f. field. If the
duration of this r.f. pulse is t, then the magnetisation will
rotate by an angle 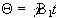 . If
that angle is 90 degrees then the pulse is referred to as a
90x pulse,
the x subscript showing that the precession is about the x' axis.
In a typical NMR experiment a 90x pulse is applied, which
tips the magnetisation vector from the longitudinal plane (parallel to
B0) to the transverse plane (perpendicular to
B0). Once in the transverse plane the magnetisation can be
detected as it precesses about the z-axis, and this is what gives rise
to the NMR signal, which is discussed in the next section.
. If
that angle is 90 degrees then the pulse is referred to as a
90x pulse,
the x subscript showing that the precession is about the x' axis.
In a typical NMR experiment a 90x pulse is applied, which
tips the magnetisation vector from the longitudinal plane (parallel to
B0) to the transverse plane (perpendicular to
B0). Once in the transverse plane the magnetisation can be
detected as it precesses about the z-axis, and this is what gives rise
to the NMR signal, which is discussed in the next section.
Since the application of a resonant r.f. pulse disturbs the spin system, there must subsequently be a process of coming back to equilibrium. This involves exchange of energy between the spin system and its surroundings. Such a process is called spin-lattice relaxation, and the rate at which equilibrium is restored is characterised by the spin-lattice or longitudinal relaxation time, T1, in a new equation of motion for Mz
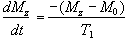
(2.27)
The spins however do not only exchange energy with the surrounding lattice, but also among themselves. This is generally a faster process than spin-lattice relaxation, and is characterised by the spin-spin relaxation time, T2, in the equations describing the evolution of Mx and My
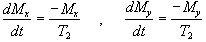 .
.
(2.28)
Equations 2.27 and 2.28, when combined with the earlier equations of motion form what are known as the Bloch equations
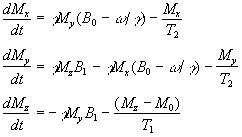
(2.29)
given here for the rotating frame of reference.
Immediately following the application of a Qx pulse, the magnetisation vector has components
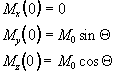
which when put in the Bloch equations give
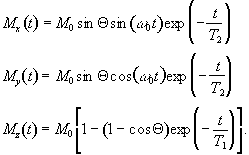 .
.
(2.30)
The relaxation times T1 and T2 are very important in imaging, as they have the greatest effect in determining contrast.
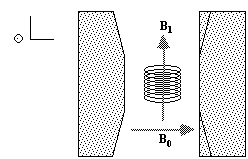
To detect the NMR signal it is necessary to have an r.f. coil which is in the transverse plane, that is perpendicular to the B0 field (Figure 2.4), in which an e.m.f. is induced which is proportional to Mx. The signal from the coil is first transformed to the rotating frame by phase sensitive detection. Normally this involves separately mixing the e.m.f. with two reference signals, both oscillating at the Larmor frequency, but 90 degrees out of phase with each other. Thus the signal detected in the coil has the form
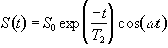
(2.31)
which after phase sensitive detection has 'real' and 'imaginary' components
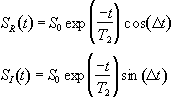
(2.32)
where D=w-w0. If w=w0 then the signal is just an exponential decay, however if w≠w0 then the signal will oscillate at a frequency D. The signal after phase sensitive detection is known as the Free Induction Decay (FID). Fourier transformation of the FID gives the value of D as shown in Figure 2.5. The width of the peak is governed by T2. This relationship is explored further in Chapter 5.
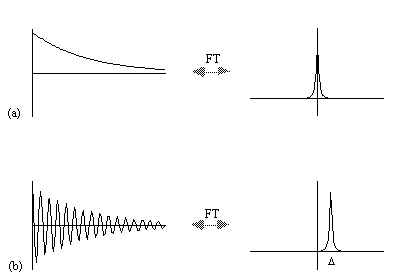
A summary of the theory of NMR as presented so far under a classical description is that, a static magnetic field, B0, polarises the sample such that it has a bulk magnetisation aligned with the direction of the field. An oscillating magnetic field at the Larmor frequency applied for a short time orthogonally to B0 will cause the longitudinal magnetisation to be tipped into the transverse plane. This makes the Larmor precession of the magnetisation under B0 detectable, and Fourier transformation of the phase sensitively detected signal yields its offset from the expected value.
It is this offset from expected value that is most useful in magnetic resonance, as the B0 field experienced by the different spins in the system is sensitive to nature of the chemical environment and can be manipulated by the application of external magnetic field gradients. The former is exploited in Magnetic Resonance Spectroscopy (MRS) and the latter in Magnetic Resonance Imaging.
The electrons that surround each nucleus can act to slightly perturb the magnetic field at the spin site. This causes the Larmor precession frequency to be modified by the chemical environment of the spin. The effect of chemical shift is described by the equation
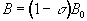
(2.33)
where s is the shielding constant. This modifies the Larmor frequency such that
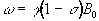
(2.34)
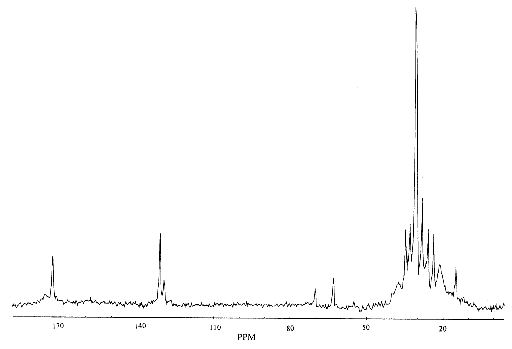
and is detected upon Fourier transformation of the FID as a shift in frequency away from that expected if chemical shift played no part. For a sample containing spins with a number of different chemical shifts, the resulting spread of frequencies represents a chemical spectrum. An example of an NMR spectrum is shown in Figure 2.6.
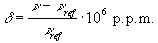
(2.35)
where n and nref are the resonant frequencies of the spectral peak of interest and the reference component respectively. Chemical shifts in 1H spectra are of the order of a few p.p.m.
Another spin effect that is useful in MRS is the scalar, or spin-spin coupling. This arises from interactions between the nuclear spins, mediated by the delocalised electrons. However this effect is not very important in imaging, since its magnitude is so small. There are a number of other features of spin behaviour which affect the NMR signal. Some of these will be described, where appropriate, in other chapters.