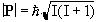
The property of Nuclear Magnetic Resonance (NMR) was first described by Purcell [1] and Bloch [2] in 1946, work for which they received the Nobel prize in 1952. Since then NMR has become a powerful tool in the analysis of chemical composition and structure. In 1973 Lauterbur [3] and Mansfield [4] used the principles of NMR to describe a technique for determining physical structure. Since then Magnetic Resonance Imaging (MRI) has been used in many biomedical, chemical and engineering applications.
In this chapter the theoretical foundations, first of nuclear magnetic resonance and then magnetic resonance imaging are explained. Then the practical implementation of MRI is outlined, and an explanation of the artefacts that affect MR images given. The chapter ends with a discussion of the safety of MRI as a medical imaging modality. This chapter serves only as an outline of the basic principles of nuclear magnetic resonance spectroscopy and imaging. More detail is found in the standard texts on the subject, such as those by Abragamm [5], and Callaghan [6].
The quantum mechanical description of atomic nuclei, as described by Dirac in 1930, predicted the property of spin angular momentum. In fact the property of electron spin was observed six years earlier by Stern and Gerlach [7], who passed a beam of neutral atoms through a non-uniform magnetic field, and observed the effect of half-integral angular momentum, that could not be explained by the previously accepted Bohr model.
This spin angular momentum is characterised by the spin quantum number I, such that the total spin angular momentum is Ih. The value of I is an intrinsic property of the nucleus, examples of which are given in Table 2.1.
| Nucleus | Spin Quantum Number I |
| 1H | 1/2 |
| 2H | 1 |
| 12C | 0 |
| 13C | 1/2 |
| 19F | 1/2 |
| 31P | 1/2 |
To exhibit the property of magnetic resonance the nucleus must have a non-zero value of I. As far as medical applications are concerned, the proton (1H) is the nucleus of most interest, because of its high natural abundance. However, other nuclei have been studied, most noticeably 13C whose low natural abundance relative to 12C makes it suitable for tracer studies.
The magnitude of the spin angular momentum is given by
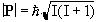
(2.1)
but since P is a vector, its orientation must be taken into account. In a magnetic field, applied along the z axis, the possible values of the z-components of the angular momentum are given by
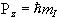
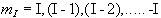 .
.(2.2)
So for the proton, with spin 1/2, there are two possible values
for 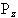 , that is
, that is 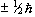 .
The eigenfunction describing
the spin state of the proton nucleus can be written as
.
The eigenfunction describing
the spin state of the proton nucleus can be written as 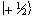 or
or  ,
and since in quantum mechanics every physical
observable has an associated operator, we can write an eigenvalue
equation to describe the observation of the spin state as
,
and since in quantum mechanics every physical
observable has an associated operator, we can write an eigenvalue
equation to describe the observation of the spin state as
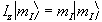
(2.3)
where  is the operator
describing measurement of the angular momentum along the z axis.
There are similar operators for measuring the angular momentum along
the x and y axes, so we have a range of eigenvalue equations for a
spin 1/2 system as follows:
is the operator
describing measurement of the angular momentum along the z axis.
There are similar operators for measuring the angular momentum along
the x and y axes, so we have a range of eigenvalue equations for a
spin 1/2 system as follows:
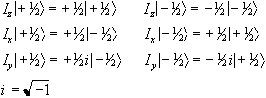
(2.4)
To measure the energy of the spin system it is necessary to construct a Hamiltonian operator. The form of the Hamiltonian can be derived from classical electromagnetism for the energy of a magnetic moment placed in a magnetic field.
Nuclei have a magnetic moment, m, which is proportional to the angular momentum,
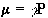
(2.5)
Nuclei with the constant of proportionality, g, being called the magnetogyric ratio. The magnetogyric ratio is a property of the particular nucleus, and has a value of 2.675 x 10 8 rad/s/T for protons. When this magnetic moment is placed in a magnetic field, B, it has energy

(2.6)
and so by combining equations 2.5 and 2.6 a Hamiltonian can be defined as
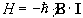 .
.
(2.7)
Since by definition the B field is applied parallel to the z-axis the Hamiltonian becomes
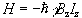
(2.8)
and is known as the Zeeman Hamiltonian. Now using the Schrödinger equation, the energy of the eigenstate is found.
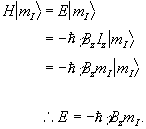
(2.9)
So for a proton with  , a transition between
the two states represents a change in energy
, a transition between
the two states represents a change in energy
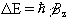
(2.10)

This is called the Zeeman splitting, and is shown as an energy level diagram in Figure 2.1. These two states are given a variety of labels, but most commonly referred to as 'spin up', and 'spin down', with the spin-down state having a higher energy than the spin-up state. Transitions between the two states can be induced by absorption or emission of a photon of frequency n 0, such that
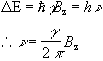
(2.11)
Expressing the frequency in angular terms gives the Larmor equation which underpins the whole of NMR
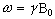
(2.12)
the characteristic frequency, w, being the Larmor frequency. The magnetic field, labelled B0, is still assumed to be applied along the z axis, and is now subscripted with a '0' to distinguish it from the applied radio frequency field which will be introduced later.
This description of the quantum mechanical behaviour of an atomic nucleus leads to the way NMR is performed. Transitions between the two energy states, spin-up and spin-down, can occur by absorption or emission of electromagnetic radiation of frequency given by the Larmor equation. This frequency depends, for a given species of nuclei, purely on the applied magnetic field. It is the strength of the field experienced by the nucleus that enables structure to be determined in spectroscopy experiments, and position to be found in imaging experiments.
In a real system there is not just one nucleus in isolation, but many nuclei all of which could occupy a particular spin state. This means that the theory must be extended to consider an ensemble of spins.
To do this a single eigenstate Y, which is a linear combination of the possible spin states for a single nucleus is defined

(2.13)
When making a measurement on such a system, the expectation value of the operation on this superposition of states is
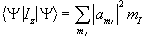
(2.14)
where the value 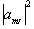 represents the probability
of finding a single nucleus in the state mI. So for
the case of a proton, with two spin states
represents the probability
of finding a single nucleus in the state mI. So for
the case of a proton, with two spin states

(2.15)
The ratio of the populations of the two energy states from Boltzman statistics is
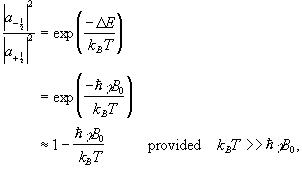
(2.16)
so the difference between the number of spins in the spin-up state and the spin-down state is

(2.17)
If we now assume that all the 'spin up' nuclei have a
magnetic moment of 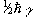 and the 'spin down'
nuclei have a magnetic moment of -
and the 'spin down'
nuclei have a magnetic moment of -![]() , then we can write the bulk magnetisation of the ensemble
as
, then we can write the bulk magnetisation of the ensemble
as
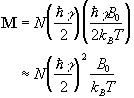
(2.18)
where N is the number of spins in the ensemble. Being able to treat the behaviour of all the spins in the system in terms of magnetisation allows a transfer from a quantum mechanical to a classical description of NMR. The advantage of the classical description is that it gives a simpler picture of the NMR experiment.
If the spin magnetisation vector M is placed in a magnetic field B, M will experience a torque. The equation of motion for M can be written
 .
.
(2.19)
If B is a static (time-independent) field along the z axis
such that  then equation 2.19 becomes
then equation 2.19 becomes
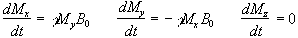
(2.20)
which has solutions
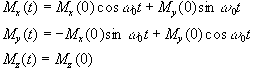
(2.21)
where 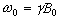 . These equations describe the
precession of the magnetisation vector about the z axis as shown in
Figure 2.2. The angular frequency of the precession is identical to
the Larmor frequency derived in the quantum mechanical description
above (equation 2.12), showing how the classical and quantum
mechanical pictures coincide.
. These equations describe the
precession of the magnetisation vector about the z axis as shown in
Figure 2.2. The angular frequency of the precession is identical to
the Larmor frequency derived in the quantum mechanical description
above (equation 2.12), showing how the classical and quantum
mechanical pictures coincide.
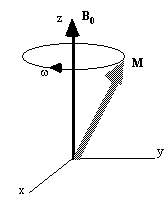
Now, as well as the static B0 field applied along z, consider a time varying field B1, applied perpendicularly to B0 and oscillating at w0. If only the circularly polarised component of B1 rotating in the same direction as the precessing magnetisation vector is considered
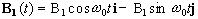
(2.22)
which when put into equation 2.19 yields

(2.23)
If a starting condition M(0)=M0k is defined, then the solutions for M are

(2.24)
where 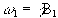 .
.
This implies that by applying an oscillating magnetic field of frequency w0, the magnetisation simultaneously precesses about B0 at w 0 and B1 at w 1, as shown in Figure 2.3a.
At this point it is appropriate to introduce a new frame of reference for viewing the evolution of the magnetisation vector, the rotating frame, which rotates about the z-axis at frequency w 0. If in the rotating frame an axis system (x',y',z) is defined then equation 2.19 can be written
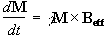
(2.25)
where
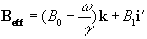
(2.26)
and (i',j',k) are unit vectors in the (x',y',z)
directions. The result of solving
these two equations is a magnetisation vector which precesses about
Beff, as
shown in Figure 2.3b. If  and M precesses about the x' axis shown in Figure 2.3c.
Applying the B1
field has the effect of rotating the magnetisation
vector about the x'-axis at an angular frequency
w1=
g
B1.
and M precesses about the x' axis shown in Figure 2.3c.
Applying the B1
field has the effect of rotating the magnetisation
vector about the x'-axis at an angular frequency
w1=
g
B1.
(a)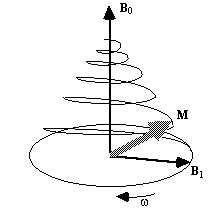
(b)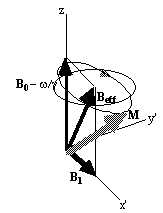
(c)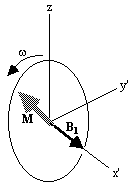
The most common way to carry out an NMR
experiment is to apply a short burst of resonant r.f. field. If the
duration of this r.f. pulse is t, then the magnetisation will
rotate by an angle  . If
that angle is 90 degrees then the pulse is referred to as a
90x pulse,
the x subscript showing that the precession is about the x' axis.
In a typical NMR experiment a 90x pulse is applied, which
tips the magnetisation vector from the longitudinal plane (parallel to
B0) to the transverse plane (perpendicular to
B0). Once in the transverse plane the magnetisation can be
detected as it precesses about the z-axis, and this is what gives rise
to the NMR signal, which is discussed in the next section.
. If
that angle is 90 degrees then the pulse is referred to as a
90x pulse,
the x subscript showing that the precession is about the x' axis.
In a typical NMR experiment a 90x pulse is applied, which
tips the magnetisation vector from the longitudinal plane (parallel to
B0) to the transverse plane (perpendicular to
B0). Once in the transverse plane the magnetisation can be
detected as it precesses about the z-axis, and this is what gives rise
to the NMR signal, which is discussed in the next section.
Since the application of a resonant r.f. pulse disturbs the spin system, there must subsequently be a process of coming back to equilibrium. This involves exchange of energy between the spin system and its surroundings. Such a process is called spin-lattice relaxation, and the rate at which equilibrium is restored is characterised by the spin-lattice or longitudinal relaxation time, T1, in a new equation of motion for Mz
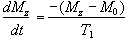
(2.27)
The spins however do not only exchange energy with the surrounding lattice, but also among themselves. This is generally a faster process than spin-lattice relaxation, and is characterised by the spin-spin relaxation time, T2, in the equations describing the evolution of Mx and My
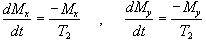 .
.
(2.28)
Equations 2.27 and 2.28, when combined with the earlier equations of motion form what are known as the Bloch equations

(2.29)
given here for the rotating frame of reference.
Immediately following the application of a Qx pulse, the magnetisation vector has components
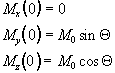
which when put in the Bloch equations give
 .
.
(2.30)
The relaxation times T1 and T2 are very important in imaging, as they have the greatest effect in determining contrast.
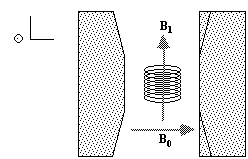
To detect the NMR signal it is necessary to have an r.f. coil which is in the transverse plane, that is perpendicular to the B0 field (Figure 2.4), in which an e.m.f. is induced which is proportional to Mx. The signal from the coil is first transformed to the rotating frame by phase sensitive detection. Normally this involves separately mixing the e.m.f. with two reference signals, both oscillating at the Larmor frequency, but 90 degrees out of phase with each other. Thus the signal detected in the coil has the form
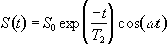
(2.31)
which after phase sensitive detection has 'real' and 'imaginary' components
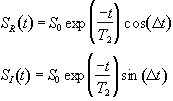
(2.32)
where D=w-w0. If w=w0 then the signal is just an exponential decay, however if w≠w0 then the signal will oscillate at a frequency D. The signal after phase sensitive detection is known as the Free Induction Decay (FID). Fourier transformation of the FID gives the value of D as shown in Figure 2.5. The width of the peak is governed by T2. This relationship is explored further in Chapter 5.
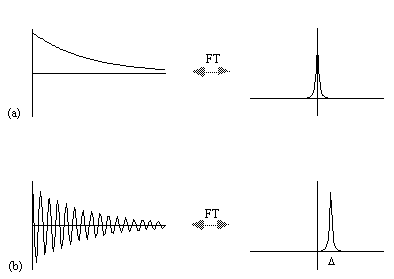
A summary of the theory of NMR as presented so far under a classical description is that, a static magnetic field, B0, polarises the sample such that it has a bulk magnetisation aligned with the direction of the field. An oscillating magnetic field at the Larmor frequency applied for a short time orthogonally to B0 will cause the longitudinal magnetisation to be tipped into the transverse plane. This makes the Larmor precession of the magnetisation under B0 detectable, and Fourier transformation of the phase sensitively detected signal yields its offset from the expected value.
It is this offset from expected value that is most useful in magnetic resonance, as the B0 field experienced by the different spins in the system is sensitive to nature of the chemical environment and can be manipulated by the application of external magnetic field gradients. The former is exploited in Magnetic Resonance Spectroscopy (MRS) and the latter in Magnetic Resonance Imaging.
The electrons that surround each nucleus can act to slightly perturb the magnetic field at the spin site. This causes the Larmor precession frequency to be modified by the chemical environment of the spin. The effect of chemical shift is described by the equation
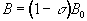
(2.33)
where s is the shielding constant. This modifies the Larmor frequency such that

(2.34)
and is detected upon Fourier transformation of the FID as a shift in frequency away from that expected if chemical shift played no part. For a sample containing spins with a number of different chemical shifts, the resulting spread of frequencies represents a chemical spectrum. An example of an NMR spectrum is shown in Figure 2.6.
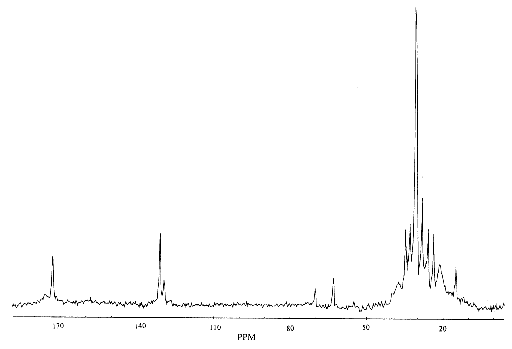
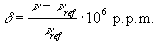
(2.35)
where n and nref are the resonant frequencies of the spectral peak of interest and the reference component respectively. Chemical shifts in 1H spectra are of the order of a few p.p.m.
Another spin effect that is useful in MRS is the scalar, or spin-spin coupling. This arises from interactions between the nuclear spins, mediated by the delocalised electrons. However this effect is not very important in imaging, since its magnitude is so small. There are a number of other features of spin behaviour which affect the NMR signal. Some of these will be described, where appropriate, in other chapters.
As has been shown in
Section 2.2, the fundamental equation of magnetic resonance is the
Larmor equation, 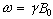 . In an
NMR experiment a measurement of the frequency of precession of the
magnetisation gives information on the field experienced by that group
of spins. By manipulating the spatial variation of the field in a
known way, this frequency information now yields spatial
information.
. In an
NMR experiment a measurement of the frequency of precession of the
magnetisation gives information on the field experienced by that group
of spins. By manipulating the spatial variation of the field in a
known way, this frequency information now yields spatial
information.
Consider a linear field gradient in B which increases along the x axis, such that
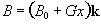
(2.36)
where G is the gradient strength. This makes the Larmor equation

(2.37)
or in its more general three dimensional form
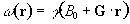
(2.38)
Under a linear field gradient along the x axis, all the spins which lie at a particular value of x will precess at the same frequency. The FID from such a sample will contain components from each of the x values represented by the sample, and the frequency spectrum will therefore represent the number of spins that lie along that plane
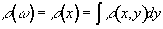
(2.39)
as shown in Figure 2.7c.
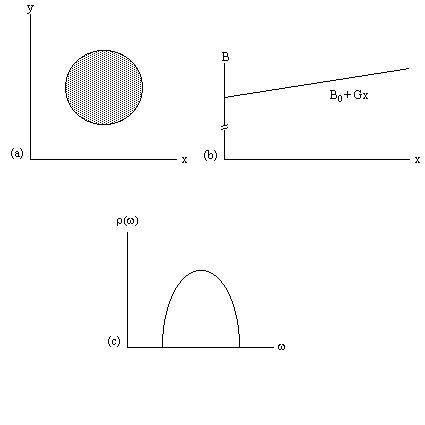
This simple spectrum therefore gives the spatial information about the object being imaged along one dimension. To build up the complete 3D image it is necessary to apply time varying field gradients. A number of methods for doing this are described later in this section, but first the notion of k-space is introduced, which is useful in describing all these techniques.
Having denoted the number of spins at a particular location r, as the spin density, r(r), the signal from the sample can be written
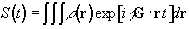
(2.40)
The reciprocal space vector is defined
(2.41)
and the Fourier relationship between signal and spin density becomes obvious

(2.41)
Thus k is the conjugate variable for r. The resolution of the image depends on the extent of k-space that is sampled, and it is by looking at how different imaging techniques cover k-space that they can usefully be compared [8]. For example in the previous section a gradient along the x-axis was applied to a cylindrical sample. This meant that values in kx could be sampled, but not in ky and so the complete 2D structure could not be obtained.
There are imaging techniques which sample all three dimensions of k space, but most techniques reduce the problem to two dimensions by applying slice selection.
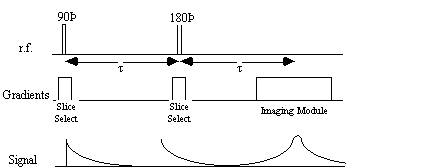
Slice selection is a technique to isolate a single plane in the object being imaged, by only exciting the spins in that plane. To do this an r.f. pulse which only affects a limited part of the NMR spectrum is applied, in the presence of a linear field gradient along the direction along which the slice is to be selected (Figure 2.8). This results in the excitation of only those spins whose Larmor frequency, which is dictated by their position, is the same as the frequency of the applied r.f. pulse.
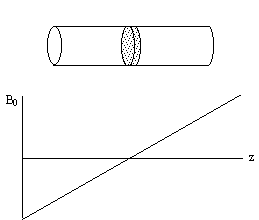
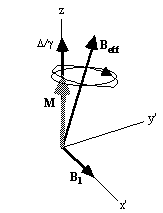
Consider an r.f. pulse of duration 2t which is applied in the presence of a gradient along some axis, say z, such that 2tgB1= p/2 (a 90 degree pulse). The spins where B=B0 (i.e. z=0) will precess into the transverse plane, whilst those where B>>B0 (i.e. z>>0) will precess about Beff=Dw/g k+B1i, and have little effect on the transverse magnetisation (Figure 2.9).
To tailor the shape of slice selected it is necessary to modulate the pulse profile. For small flip angles the relationship between the pulse modulation and slice profile can be derived. To do this consider applying an r.f. pulse lasting from t=-T to +T, to a sample in a gradient Gz. The Bloch equations as shown earlier (equation. 2.29) in the rotating frame, neglecting T1 and T2 relaxation, become
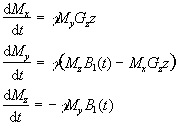
(2.43)
Now these are transformed to another frame of reference which rotates at angular frequency gGzz. Each slice will have a different reference frame, depending on the value of z, but considering just one of these gives
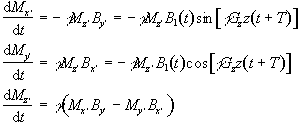
(2.44)
with the two reference frames coinciding at t=-T. If the assumption is made that the flip angles are small then it is possible to say that Mz' varies very little, and takes the value M0. So equations 2.44 become

(2.45)
If Mx and My are treated as real
and imaginary parts of the complex magnetisation 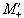 , the equation of motion becomes
, the equation of motion becomes
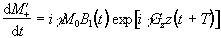
(2.46)
By integrating and converting back to the original (rotating) frame of reference, since

gives

(2.47)
This is the Fourier transform of the r.f. pulse profile, so a long pulse gives a narrow slice and vice-versa. This equation also shows one other thing about the magnetisation in the slice after the pulse. There is a phase shift through the slice of gGzzT which will cause problems for imaging later. This can be removed by reversing the gradient Gz for a duration T, which is known as slice refocusing.
To excite a sharp edged slice, the r.f. pulse modulation required is a sinc function. For practical implementation of this kind of pulse it is necessary to limit the length of the pulse, and so usually a five lobe sinc function is used. The above approximation is only correct for small pulse angles. For larger flip angles, it is hard to analytically determine the pulse modulation required for a desired slice profile, and so it is usually necessary to use some form of iterative method to optimise pulses [9]. Using such techniques it is possible to design a range of pulses which are able to select different slice profiles and carry out other spin manipulation techniques such as fat or water suppression. It is also possible to design pulses which do not require refocusing [10]. Usually the limit in such novel designs is their practical implementation, and so the most common three pulse modulations used are a 'hard' pulse, with top-hat modulation, a Gaussian modulation or a 'soft' pulse, with truncated sinc modulation.
If any slice other than the central (B=B0) slice is required, then the frequency of oscillation can be altered and the slice selected will be at the position along the z-axis given by
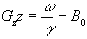
(2.48)
The extensively used techniques in MRI are all Fourier based, that is the 'spin-warp' technique and Echo Planar Imaging (EPI) [11]. However the early MR images used point and line methods and these are described here, along with the technique of projection reconstruction.
The f.o.n.a.r. technique (field focused nuclear magnetic resonance) was proposed by Damadian, and was used to produce the first whole body image in 1977 [12]. The basis of the technique is to create a shaped B0 field which has a central homogeneous region, surrounded by a largely inhomogeneous region. The signals from the inhomogeneous regions will have a very short T2* and can thus be distinguished from the signal from the homogeneous region. By scanning the homogeneous field region across the whole of the sample an image can be made up. This is a time consuming procedure taking tens of minutes for a single slice. The two advantages of the technique are its conceptual simplicity and the lack of a requirement for the static field to be homogeneous over a large area. Shaped r.f. pulses can also be used to isolate a small region, and such methods form the basis of localised spectroscopy.
As was shown in section 2.3.1, if we have only a one dimensional object then a single linear gradient is sufficient to locate position directly from the FID by Fourier transformation. If then the three dimensional sample can be reduced to a set of one dimensional components then the whole sample can be imaged. This can be done by selective irradiation, or slice selection, in two of the dimensions. First, in the presence of a gradient along the z-axis, a selective pulse is applied which saturates all the spins outside the plane of interest (Figure 2.10a). Then a gradient is applied along the x-axis, and those spins not saturated are tipped into the transverse plane by a selective 90 degree pulse (Figure 2.10b). Immediately after the second r.f pulse the only region with any coherent transverse magnetisation is the line of intersection of the two selected planes. A gradient is now applied along the y-axis, and the evolution of the FID recorded. Fourier transform of the FID gives the proton densities along that line. By repeating the line selection for all the lines in the plane, an image of the whole of the plane can be built up. There are many variations of the line scan technique, some of which utilise 180 degree pulses, but they are inefficient in comparison to the Fourier methods discussed in the next section.
(a) 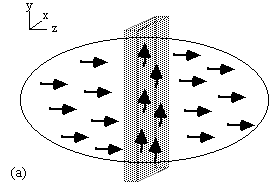 (b)
(b) 
One final method of interest is projection reconstruction. This is the method used to build up X-ray CT scans [13], and was the method used to acquire the early MR images. Following slice selection, a gradient is applied along the x-axis and the projections of the spin densities onto that axis obtained by Fourier transformation of the FID. Then a linear gradient is applied along an axis at some angle to the x-axis, q. This can be achieved by using a combination of the x and y gradients
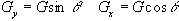 .
.
(2.49)
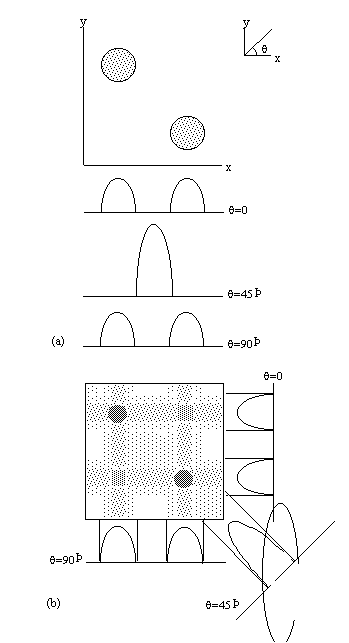
Projections are taken as q is incremented up to 180 degrees (Figure 2.11a). The set of projections can then be put together using back projection. This distributes the measured spin densities evenly along the line normal to the axis it was acquired on. By reconstructing all the angled projections the image appears. There is however a blurred artefact across the whole image, where an attempt was made to assign spin density to areas where there is in fact none, and star artefacts where a finite number of projections have been used to define point structures. This can be corrected using a technique called filtered back projection, which convolves each of the profiles with a filter
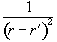
(2.50)
This is done in the Fourier domain by dividing the Fourier projections by the modulus of the vector k as defined in section 2.3.2.
Projection reconstruction has been largely superseded by methods which sample k-space more uniformly.
Quadrature detection of the FID means that the phase as well as the frequency of the signal can be recorded. This is utilised in the Fourier techniques described in this section.
The 'spin-warp' method (often called 2DFT) as described by Edelstein et. al. [14] is a development of the earlier technique of Fourier zeugmatography proposed by Kumar, Welti, and Ernst [15]. The Fourier zeugmatography sequence can be split into three distinct sections, namely slice selection, phase encoding, and readout. The pulse sequence diagram for the sequence is shown in Figure 2.12. Such diagrams are commonly used to describe the implementation of a particular MR sequence, and show the waveform of the signal sent to the three orthogonal gradient coils and the r.f. coil.
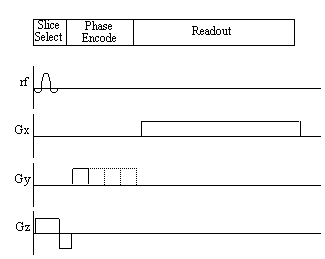
Having excited only those spins which lie in one plane, a gradient is applied along the y-axis. This will cause the spins to precess at a frequency determined by their y position, and is called phase encoding. Next a gradient is applied along the x-axis and the FID is collected. The frequency components of the FID give information of the x-position and the phase values give information of the y-position.
More specifically, if a gradient of strength Gy is applied for a time ty during the phase encoding stage, and then a gradient Gx is applied for a duration tx the signal recorded in the FID is given by
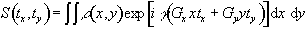
(2.51)
By writing  equation (2.51) becomes
equation (2.51) becomes

(2.52)
so the single step is equivalent to sampling one line in the kx direction of k-space. To cover the whole of k-space it is necessary to repeat the sequence with slightly longer periods of phase encoding each time (Figure 2.13).
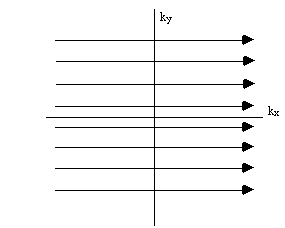
Having acquired data for all values of kx and ky, a 2D Fourier transform recovers the spin density function
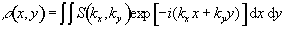
(2.53)
Figure 2.14 illustrates how the magnetisation evolves under these two gradients.

One drawback of this technique is that the time between exciting the spins, and recording the FID varies throughout the experiment. This means that the different lines in the ky direction will have different weighting from T2* magnetisation decay. This is overcome in spin-warp imaging by keeping the length of the y gradient constant for each acquisition, and varying ky by changing the gradient strength. The pulse diagram for this technique is shown in Figure 2.15.

It is desirable to have as much signal as possible for each FID, and a necessity that the amount of transverse magnetisation available immediately after the r.f. pulse is the same for each line. This can be a problem since the recovery of longitudinal magnetisation is dependent on spin-lattice relaxation, and T1 values in biomedical imaging are of the order of seconds. Keeping the time between adjacent spin excitations, often known as TR, the same throughout the image acquisition will keep the transverse magnetisation the same for each FID, provided the first few samples are discarded to allow the system to come to a steady state. Leaving the magnetisation to recover fully, however, would be very costly in time, so it is usually necessary to have a TR which is less than T1. To maximise the signal received for small TR values it is possible to use a smaller flip angle than 90 degrees. The transverse magnetisation that is available after such a pulse is less than it would be after a 90 degree pulse, but there is more longitudinal magnetisation available prior to the pulse. To optimise the flip angle q, for a particular TR, we first assume that the steady state has been reached, that is that
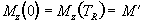
(2.54)
Now the magnetisation is flipped by a q degree pulse, and the z-magnetisation becomes
 .
.
(2.55)
The recovery of the magnetisation is governed by the equation

(2.56)
which can be integrated to find M',

(2.57)
The transverse magnetisation following the pulse, which we want to maximise, is given by
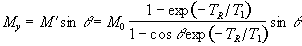
(2.58)
which has its maximum value when
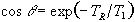
(2.59)
The angle this occurs at is known as the Ernst angle [16]. The amount of signal available is very dependent on the repetition time TR. For example, if a sample has a T1 of 1s, then at a TR of 4s M'=0.98M0, however as TR is reduced to 500ms, M'=0.62M0.
If a 3D volume is to be imaged then it is possible to acquire extra slices with no time penalty. This is because it is possible to excite a separate slice, and acquire one line of k-space, whilst waiting for the longitudinal magnetisation of the previous slice to recover. This technique is called multi-slicing.
The common implementation of the spin-warp technique, FLASH (Fast Low-Angle SHot imaging) [17], uses very small flip angles (~5 degrees) to run at with a fast repetition rate, acquiring an entire image in the order of seconds.
In Echo Planar Imaging [18, 19] (EPI) the whole of k-space is acquired from one FID. This is possible because, having acquired one set of frequency information, the sign of the readout gradients can be reversed and the spins will precess in the opposite direction in the rotating frame (Figure 2.16) and subsequently rephase causing a regrowth of the NMR signal. This is a called a gradient echo. By switching the readout gradient rapidly, the whole of k-space can be sampled before spin-spin (T2) relaxation attenuates the transverse magnetisation. Phase encoding is again used in order to sample ky.
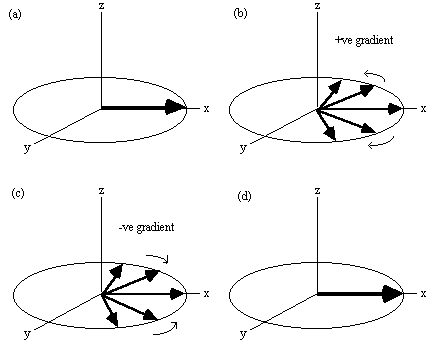
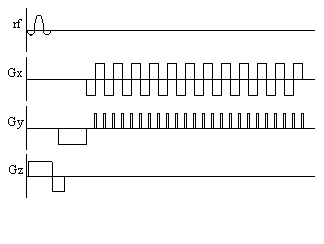
The three gradients in EPI are usually labelled the slice select (z), blipped (y) and switched (x), because of their respective waveforms. Echo planar imaging is a technically demanding form of MRI, usually requiring specialised hardware, however it has the advantage of being a very rapid imaging technique, capable of capturing moving organs like the heart, and dynamically imaging brain activation. This is only a brief introduction to EPI, since its strengths and limitations are discussed in more detail in the following chapters.
There are numerous variations on the basic MRI sequences described above. Several of them, notably interleaved EPI, are explained in other chapters. Other important sequences are outlined here.
It was shown in the previous section how phase encoding enabled the information on the second dimension to be added to the one dimensional line profile. It is possible to extrapolate this procedure to the third dimension by introducing phase encoding along the z axis. Thus the 2D-FT technique is extended to a 3D-FT technique [20]. All such volumar imaging sequences first involve the selection of a thick slice, or slab. Then phase encoding is applied in the z-direction and the y-direction, followed by a readout gradient in the x-direction, during which the FID is sampled. The assembled FID's are then subject to a three dimensional Fourier transform yielding the volume image. Phase encoding can also be used in EPI instead of multi-slicing. The slice select gradient and r.f. pulse being replaced by a slab selective pulse and a phase encoding gradient along the z-axis.
Going even further, it is possible to acquire all the data to reconstruct a 3D volume from one FID, in the technique called Echo Volumar Imaging (EVI) [21]. This uses another blipped gradient in the z direction, as shown in Figure 2.18. The limitation in EVI is the need to switch the gradients fast enough to acquire all the data, before T2* destroys the signal.
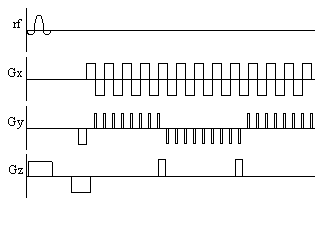
Often the main limitation in implementing fast imaging sequences such as EPI is switching the gradients at the fast rates required. A sequence which is similar to EPI, but slightly easier to implement is spiral imaging. This covers k-space in a spiral from the centre outwards, which requires sinusoidal gradients in x and y, increasing in amplitude with time. Such gradient waveforms are easier to produce than the gradients required for EPI. Spiral imaging also has the advantage of sampling the centre of k-space first, and so the low spatial frequencies, that affect the image the most are sampled first, when the signal has not been eroded by T2*. The pulse sequence diagram and coverage of k-space for spiral imaging are shown in Figure 2.19.
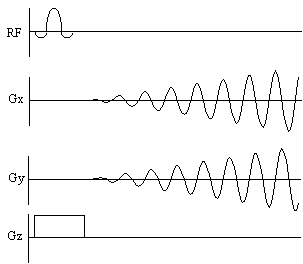
In general imaging, the chemical shifts of the protons are ignored, and usually seen only as an artefact. However it is possible to image the chemical shifts, which gives not only spatial information but also spectral information. The technique, called Chemical Shift Imaging (CSI) [22], treats the chemical shift as an extra imaging gradient in the fourth dimension. By introducing a variable delay between the excitation pulse and imaging gradients, the chemical shift 'gradient' will phase encode in this direction. Fourier transformation in this case gives the conventional NMR spectrum.
Finally, it is possible to image nuclei other than the proton. Sodium, phosphorus and carbon-13 have all been used to form biomedical images. In the case of 13C, its low natural abundance makes it useful for tracer studies.
Unlike many other medical imaging modalities, the contrast in an MR image is strongly dependent upon the way the image is acquired. By adding r.f. or gradient pulses, and by careful choice of timings, it is possible to highlight different components in the object being imaged. In the sequence descriptions that follow it is assumed that the imaging method used is EPI, however identical or similar methods can be used with the other MR imaging techniques outlined above.
The basis of contrast is the spin density throughout the object. If there are no spins present in a region it is not possible to get an NMR signal at all. Proton spin densities depend on water content, typical values of which are given in Table 2.2 for various human tissues [23]. The low proton spin density of bone makes MRI a less suitable choice for skeletal imaging than X-ray shadowgraphs or X-ray CT. Since there is such a small difference in proton spin density between most other tissues in the body, other suitable contrast mechanisms must be employed. These are generally based on the variation in the values of T1 and T2 for different tissues.
| Tissue | % Water Content |
| Grey Matter | 70.6 |
| White Matter | 84.3 |
| Heart | 80.0 |
| Blood | 93.0 |
| Bone | 12.2 |
When describing the effect of the two relaxation times on image contrast, it is important to distinguish between relaxation time maps, and relaxation time weighted images. In the former the pixel intensities in the image have a direct correspondence to the value of the relaxation time, whilst in the latter the image is a proton density image which has been weighted by the action of the relaxation.
The spin-lattice relaxation time T1, is a measure of the time for the longitudinal magnetisation to recover. A proton density image can be weighted by applying an r.f. pulse which saturates the longitudinal magnetisation prior to imaging. Spins that have recovered quickly will have greater available z-magnetisation prior to imaging than those which recover slowly. This effect is apparent if the same slice, or set of slices, are imaged rapidly, because the excitation pulse of the previously imaged slice affects the magnetisation available for the current slice. More commonly however, if T1 maps, or T1 weighted images are required then the imaging module is preceded by a 180 degree pulse (Figure 2.20). The 180 degree pulse will invert the longitudinal magnetisation, whilst not producing any transverse magnetisation. The recovery of the longitudinal magnetisation is governed by the Bloch equation for Mz, which has the solution
 .
.
(2.60)
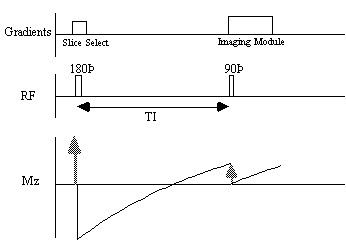
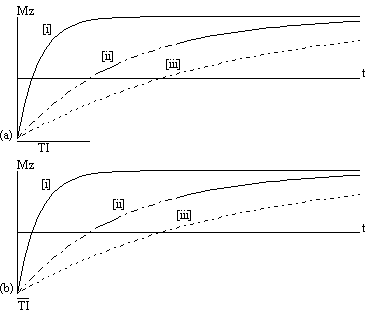
The magnetisation is allowed to recover for a time TI, after which it is imaged using a 90 degree pulse, and usual imaging gradients. The amount of signal available will depend on the rate of recovery of Mz. If, as in Figure 2.21, the sample has spins with several different relaxation times, it is possible to choose TI such that the signal from spins with one recovery curve is nulled completely, whilst giving a good contrast between spins with other recovery curves. Figure 2.22 shows some examples of T1 weighted images. In order to calculate the values of T1, to create a T1 map, it is necessary to obtain a number of points along the magnetisation recovery curve, and then fit the points to the equation 2.60. The most straightforward way to do this is to repeat the inversion recovery sequence for a number of values of TI, but there are techniques which acquire all the data in a single recovery curve [24, 25].
(a) 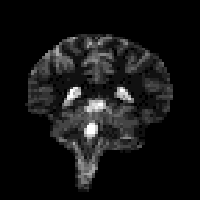 (b)
(b) 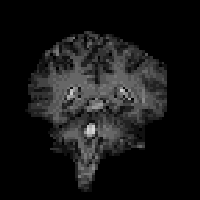
The problem with measuring T2 with a sequence which relies on a gradient echo (as EPI does) is that there is a confounding effect which erodes the transverse magnetisation in the same way that spin-spin relaxation does, which is that of field inhomogeneities. If the spins in a single voxel do not experience exactly the same field, then the coherence of their magnetisation will be reduced, an effect which increases with time. The combined effect of spin-spin relaxation and an inhomogeneous field on transverse magnetisation is characterised by another time constant T2*, and the decay of the signal is governed by the equation
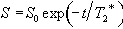
(2.61)
In fact T2* weighted images are desirable for functional MRI applications, as is explained in the next chapter. To change the T2* weighting of an image, it is only necessary to change the time between the excitation pulse and the imaging gradients. The longer the delay, the greater the T2* weighting, as shown in Figure 2.23. Examples of T2* weighted images are shown in Figure 2.24. T2* maps can be obtained by taking several images with different delays, and fitting to equation 2.61. A technique for obtaining T2* maps from a single FID is explained in Chapter 4.

(a)  (b)
(b)
It is possible to obtain the real value of T2 by refocusing the effect of field inhomogeneity on the transverse magnetisation using a spin-echo. A spin-echo is formed by applying a 180 degree pulse, a time t after the excitation pulse. This has the effect of refocusing the signal at time 2t (Figures 2.25, 2.26).
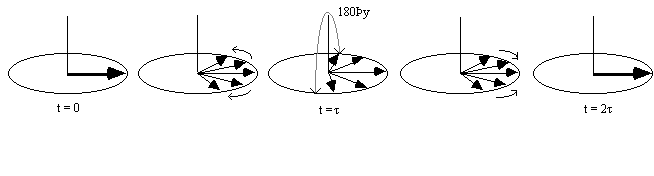
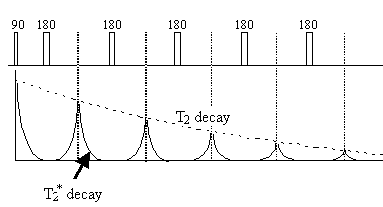
Since the spin-spin relaxation is not refocused in the spin echo, the contrast in the image is dependent on T2 and not T2*, with contrast being dependent on the delay between the excitation pulse and the imaging module. Again T2 maps can be made from images with different delay times (called the echo time, TE), by fitting to the T2 decay equation which is similar to equation 2.61. Multiple echoes can be formed by using a series of 180 degrees pulses as shown in Figure 2.27.
In order to improve the contrast of images, it is common to use some form of contrast agent. The most common of these in MRI is gadolinium, which is a paramagnetic ion, and reduces the spin-lattice relaxation time (T1) considerably.
One of the usual assumptions about imaging using magnetic resonance is that the spins are stationary throughout the imaging process. This of course may not be true, for example if blood vessels are in the region being imaged. Take for example the situation of imaging a plane through which a number of blood vessels flow. A slice is selected and all the spins in that slice are excited, however in the time before imaging, spins in the blood have flown out of the slice and unexcited spins have flown in. This means that there may be no signal from the blood vessels.
In order to measure the rate of flow, some kind of phase encoding that is flow sensitive can be applied. This is done by applying a magnetic field gradient along the direction in which flow is to be measured. A large gradient dephases the spins depending on their position along the gradient. This gradient is then reversed, which will completely rephase any stationary spins. Spins that have moved however will not be completely rephased (Figure 2.28). If the flow is coherent within a voxel, when the spins are imaged the phase difference can be calculated, and by varying the time between the forward and reverse gradients the flow can be calculated. Diffusion is measured in a similar way, but since the motion of the spins within the voxel is not coherent, the effect of diffusion is simply to diminish the signal.

As with any imaging modality, magnetic resonance images suffer from a number of artefacts. In this section, a number of the common artefacts are described, together with ways by which they can be reduced.
(a)  (b)
(b) 
(c) 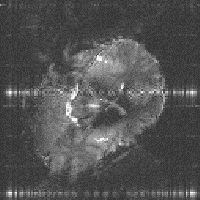 (d)
(d) 
(e) 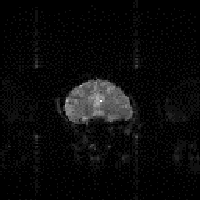 (f)
(f) 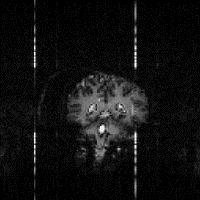
The basic assumption of MRI is that the frequency of precession of a spin is only dependent on the magnitude of the applied magnetic field gradient at that point. There are a two reasons why this may not be true.
Firstly, there is the chemical shift. This has the effect of shifting the apparent position in the image of one set of spins relative to another, even if they originate from the same part of the sample. The chemical shift artefact is commonly noticed where fat and other tissues border, as in the image of a brain in Figure 2.29a, where the fat around the skull forms a shifted 'halo'. The artefact can be removed by spin suppression, such that a selective pulse excites only the protons in the fat [26]. When the image excitation pulse is subsequently applied, the fat spins are already saturated, and so do not contribute to the image.
Secondly, the static magnetic field (B0) may not be perfectly homogeneous. Even if the magnet is very well built, the differences in magnetic susceptibility between bone, tissue and air in the body, means that the local field is unlikely to be homogeneous. If the susceptibility differences are large, such that the local magnetic field across one voxel varies by a large amount, then the value of T2* is short and there is little or no signal from such voxels. This effect is particularly evident if any metal object is present as shown in Figure 2.29b. If the differences are smaller, and the field is affected over a few voxels, then the effect is a smearing out of the image, as shown in Figure 2.29c as the altered field is interpreted as a difference in position. In 2DFT techniques susceptibility distortions occur in the readout direction, whereas in EPI they occur in the phase encoding, that is blipped, direction. The reason for this is because these are the directions in which the frequency separation of pixels is smallest. In EPI this separation can be very small so that even a small change in precessional frequency may be detected.
To reduce the artefact it is possible to locally correct the field using a set of shim coils. These apply shaped fields across the sample and in combination increase homogeneity. Susceptibility artefact is more apparent in the rapid imaging methods such as EPI and FLASH, and is difficult to reduce without losing the fast imaging rates. One way to reduce the distortion is to acquire two images with the phase encoding applied in opposite directions. The distortions will likewise be in opposite directions and a mathematical correction can be calculated and applied [27]. This topic is covered in more detail in Chapter 5.
When using any digital technique, the question of sampling occurs. One of the most important theories in digital sampling is the Nyquist sampling theorem, which states that the highest frequency that can be sampled accurately is given by
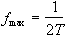
(2.62)
where T is the interval between sampling points. If the FID contains a frequency component fmax+D then it will appear to have a frequency fmax-D. This manifests itself as 'wrap-around' of the image onto itself. It is possible to reduce this problem in the readout, or switched, direction by using a band-pass filter to cut out any frequencies that could alias. In the phase encode, or blipped direction, it is necessary to ensure that there are enough sample points for the amount of phase encoding applied. An alternative is to suppress the signal from outside the field of view, using selective r.f. excitation [28].
There are three further artefacts due to sampling, one specific to 2DFT techniques, and the other two specific to EPI. Firstly, subject motion during the scan causes localised banding. This is not a problem in EPI since the image is acquired in a fraction of a second, but is in the slower sequences such as spin-warp. Depending on the source of the movement, there are a number of solutions. Cardiac or respiratory gating, where the scanning is locked to a particular phase of the respective cycles, is often employed to image the heart. These cycles can be monitored directly, for example using the ECG, or by sampling the phase of the NMR signal just prior to gradient application, known as a navigator echo [29].
Echo planar imaging suffers from a different type of sampling artefact, known as the Nyquist, or N/2 ghost. This is because, in EPI adjacent lines in k-space are sampled under opposite read gradients. If there is any misalignment in sampling, or differences in positive and negative gradients, then there is an alternate line modulation in k-space, which leads to a 'ghosting' of the image, as shown in Figure 2.29d. If the aliased image and the actual image overlap, then banding or fringes appear. The Nyquist ghost can be corrected to a certain extent by applying various phase corrections to the data. One such method acquires a second image with the starting direction of the switched gradient reversed to calculate the phase correction, and is described in more detail in Chapter 4.
Finally, since in EPI to switch the sign of the gradients so rapidly is difficult, the waveform of the switched gradient will not be square. In fact it is common to use a sinusoidal gradient waveform. If simple linear sampling of the signal is used with a sinusoidal gradient a complex ripple artefact in the switched direction is formed. To correct for this, the signal is usually over-sampled and then the points re-gridded to account for the sinusoidal nature of the gradients. Alternatively the sampling points can be distributed sinusoidally, sampling most densely at the peak of the gradient [30].
There are two artefacts that result from using a Fourier transform to create the image. The first is truncation artefact, which is due to the finite number of sampling points used. It is noticeable if there is a sharp intensity change in the image. Instead of a sharp edge in the image there is 'ringing', that is light or dark lines parallel to that edge. The only way to overcome this is to use more sample points.
Another effect is the central point artefact. This is due to the constant DC offset of the FID, which upon Fourier transformation becomes a central bright dot (as shown in Figure 2.29e). This can be reduced by attempting to remove the DC component from the FID, by assuming that the extremities of k-space are unlikely to contain much signal. So the first or last few lines are averaged together and this average is subtracted from all the data. Alternatively, the point can be removed cosmetically by replacing it by the average of surrounding pixels.
One final artefact to mention is that of external r.f. interference. If there is any r.f. radiation at the frequency of the receiver then it will be picked up and appear as a bright dot in the image. The best way to remove this, is to remove all potential interference from the scanner by placing it in a screened room. Figure 2.29f shows r.f. interference from a single frequency that appears as four bars in the echo planar image. The single frequency appears in four regions due to the reversal of the echo acquisition in the alternate lines, and the fact that the quadrature detection has identified both positive and negative components of the signal. The spreading out of the points to bars, is because sinusoidal sampling was employed. A method for removing this artefact from non-linearly sampled images is described in Chapter 4.
An MRI scanner is made up of four components: the magnet, gradient coils, r.f. transmitter and receiver, and the computer. In this section the general design and construction of these components is discussed. More specific details of the system used for the experiments in this thesis are given in the relevant chapters.
The magnet is the most expensive part of the whole scanner. The earliest systems were based around water-cooled resistive magnets, and for particular applications it is possible to use permanent magnets, but the majority of modern scanners use superconducting magnets. The reason for this is the high fields now desirable for MRI. Whole body resistive and permanent magnets are limited to around 0.3 T field strength, before their weight becomes prohibitively large. Superconducting magnets are able to generate much larger fields, and there are a number of 4.0 T whole body scanners now available. These magnets are constructed from materials such as NbTi alloy, which below a critical temperature of about 9 K loses its resistivity. Once started the current will flow in the coils indefinitely, provided that the temperature is kept below the critical temperature by cooling with liquid helium. The fields from such magnets are very stable with time, which is essential for an MRI system.
Of course one of the most important requirements for NMR is that the field is as homogeneous a possible, with tolerances as low as 1 p.p.m. required over the volume of interest. For this purpose, upon installation, the field is evened out as much as possible using ferromagnetic blocks placed inside the bore. As well as this, a set of resistive coils known as shim coils, are place within the bore of the magnet. These generate fields that vary with a particular function of position. Using these in combination it is possible to improve not only on the intrinsic homogeneity of the magnet, but also reduce the field effects due to susceptibility differences in the object being scanned.
The requirement of the gradient coils are twofold. First they are required to produce a linear variation in field along one direction, and secondly to have high efficiency, low inductance and low resistance, in order to minimise the current requirements and heat deposition.
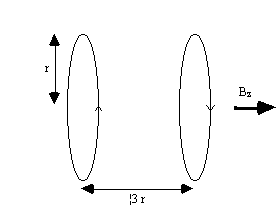
Linear variation in field along the direction of the field (traditionally labelled the z-axis) is usually produced by a Maxwell coil. This consists of a pair of coils separated by 1.73 times their radius as shown in Figure 2.30. Current flows in the opposite sense in the two coils, and produces a very linear gradient.
To produce a linear gradient in the other two axes requires wires running along the bore of the magnet. This is best done using a saddle-coil, such as the Golay coil shown in Figure 2.31. This consists of four saddles running along the bore of the magnet which produces a linear variation in Bz along the x or y axis, depending on the axial orientation. This configuration produces a very linear field at the central plane, but this linearity is lost rapidly away from this. In order to improve this, a number of pairs can be used which have different axial separations. If a gradient is required in an axis which is not along x,y or z, then this is achievable by sending currents in the appropriate proportions to Gx, Gy and Gz coils. If for example a transverse gradient G at an angle q to the x-axis is required, then a gradient Gcosq should be applied in the x direction, and Gsinq in y.

The magnitudes of the currents required, and the appropriate
waveforms are digitally generated, and converted into analogue
voltages. These are fed into power amplifiers which produce the
10's of amps required to generate the appropriate gradients. With
a technique such as EPI, the readout gradient is switched from
positive to negative at rates of anything up to 5kHz. This can be
made easier by employing resonant driving of the gradient coils. To
do this a large capacitor is placed in series with the coil, which
itself is an inductor. Such a circuit has a resonance at a frequency
of 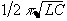 , where L is the
inductance of the coil and C is the capacitance of the series
capacitor. When driving the coil at this frequency energy is
transferred between the capacitor and the inductor, thereby reducing
the load on the power amplifier.
, where L is the
inductance of the coil and C is the capacitance of the series
capacitor. When driving the coil at this frequency energy is
transferred between the capacitor and the inductor, thereby reducing
the load on the power amplifier.
The third main component of an MRI scanner is the r.f. coil. There are many different designs of coils, but they fall into two main categories; surface coils and volume coils.
As the name suggests, a surface coil rests on the surface of the object being imaged. In its simplest form it is a coil of wire with a capacitor in parallel. The inductance of the coil, and the capacitance form a resonant circuit which is tuned to have the same resonant frequency as the spins to be imaged. In practice, since the coil is connected to a power amplifier which will have an output impedance of 50W, and the coil will have an input impedance of the order of kilo-ohms, then on transmission a lot of the power will be reflected back. To overcome this, a second capacitor is added in series with the coil, as shown in Figure 2.32, so as to match the coil impedance to 50W.
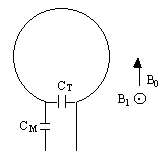
The homogeneous field produced by a simple surface coil like this is small, with the depth of penetration depending on the size of the coil. This however represents the main advantage of using a surface coil for imaging areas which lie close to the surface, as a good signal to noise ratio is achieved by inherently excluding noise signal from outside the region of interest. There are many designs of surface coil, and other localised coils for specific purposes. If however whole body images are required, or the regions of interest are far from the surface then a volume coil must be used.
Volume coils are large enough to fit either the whole body, or one specific region, such as the head or a limb, and have a homogeneous region which extends over a large area. The most commonly used design is a birdcage coil [31], as shown in Figure 2.33. This consists of a number of wires running along the z-direction, arranged to give a cosine current variation around the circumference of the coil.

The frequency supply is generated by an oscillator, which is modulated to form a shaped pulse by a double balanced mixer controlled by the waveform generator. This signal must be amplified to 1000's of watts. This can be done using either solid state electronics, valves or a combination of both.
It is possible to use the same coil to transmit and receive, or to use two separate coils. Either way it is necessary to gate the receiver side of the electronics. This is to prevent the excitation pulse, which is of the order of kilovolts, saturating or breaking the receiver electronics which are designed to detect signals of millivolts. This can again be done in a number of ways, but one such circuit for doing so is shown in Figure 2.34.

During the transmission pulse both sets of diodes will conduct, and the receiver is effectively shorted out. The short circuit at point B however looks like an open circuit at point A and so all the power is transmitted to the coil. The signal induced from the sample is too small to bias the diodes, and so is detected by the receiver circuitry.
The tiny e.m.f.'s from the sample are amplified at various stages and then mixed with a reference r.f. signal in a phase sensitive detector (p.s.d). Quadrature detection requires two p.s.d.'s, with a difference in phase of the reference signal of 90 degrees between them.
All the control of the scanner is handled by a computer. A schematic diagram of the whole system is shown in Figure 2.35.

The scanning operation is controlled from a central computer. This specifies the shape of gradient and r.f. waveforms, and timings to be used, and passes this information to the waveform generator, which outputs the signals and passes them to be amplified and sent to the coils. The NMR signal, once it has been phase sensitively detected, is turned to a digital signal by an analogue to digital converter. The digital signal is then sent to an image processor for Fourier transformation and the image is displayed on a monitor.
The raw data, that is the signal before Fourier transformation, is stored to enable the application of corrections to the data in post processing. To allow the use of fast Fourier transformation, matrix sizes of 2n are usually used.
Since the technique of MRI is used to image humans, it is important to keep the safety of the subjects as a high priority. Since MRI does not use any form of ionising radiation, it is considerably safer than x-ray or radio-isotope techniques. However it is important, especially in a research setting, that the potential hazards of any new developments are carefully considered. In this section the major safety aspects are outlined.
Most scanners used for MRI use magnets with field strengths of anything from 0.1 T to 4 T. There are many opinions on the effect of magnetic fields on biological tissues, and many studies carried out on the subject, ranging from epidemiological human studies, to the investigation of the development of animal embryos in high fields [32]. It is however currently concluded that there is no adverse biological effect from the static magnetic field used in MRI. Further experimentation will no doubt be carried out, and this view can be altered in the light of any new discoveries.
By far the more serious effect of the static magnetic field is the response of ferromagnetic objects to such fields. It is essential that no free ferromagnetic object is allowed near the magnet since the field will turn it into a projectile. In a laboratory setting this means that most tools, connectors, and other equipment to be used in the vicinity of the field must not be ferromagnetic. Subjects must be screened for objects like keys, pens, belts and other metal on clothing, as well as the possibility of surgical implants. Before scanning a subject it is also necessary to check that there would be no ill effects from exposure to the magnetic field. It is common to exclude people who are in the early stages of pregnancy, people who may have any kind of metal fragments in them, and those suffering from certain conditions such as epilepsy.
As well as the high static magnetic field used in MRI, it is possible that the two time varying fields, namely the gradients and the r.f. radiation, could affect the subject in the scanner.
The rapid switching of the field gradients, particularly in EPI, produce two safety concerns. Firstly there is the possibility of inducing voltages in tissue by Faraday's law. The current induced in a loop of tissue is dependent on the rate of change of the field (dB/dT), the conductivity of the tissue, and the cross section of the loop. Calculations by Mansfield and Morris [33] show that for dB/dT = 1.0 Ts-1, the currents induced are of the order 1 mAcm-2. Cohen [34] reports of subjects experiencing mild neural stimulation at gradient field variations of 61 Ts-1, which is higher than the rates in normal use. It is wise however, if high switching rates are used, that subjects are warned of the possible effects, and monitored during the imaging.
A second safety concern with the gradients is that of acoustic noise levels. Since large currents are flowing through wires in a large magnetic field, a force is exerted on the wires. When the currents oscillate at audio frequencies, the resulting noise can be in excess of 100 dB. Subjects therefore must wear suitable ear protection during scanning, to reduce the noise to an acceptable level.
The heat that can be dissipated by r.f. fields is a further source of concern. The currents induced in tissues by such fields are dissipated as heat. Although most tissue has adequate blood flow to carry the heat away, some anatomical regions such as the eye do not. It is sensible to keep the heating due to r.f. radiation to a minimum, and the NRPB [35] guidelines state that the body temperature, or any mass of tissue, should not rise by more than 1 degrees centigrade. This is achieved by limiting the mean absorption rate in the whole body to 0.4 Wkg-1 and in any mass of tissue to 4 Wkg-1.
It is also essential that there are no conductive items touching the subject's skin, since the heating of such objects by the r.f. radiation can cause serious burns.
Claustrophobia, and other psychological problems, can prevent a subject from being able to enter the scanner, and should be screened for before attempting to scan. It is necessary to check the subject is fully informed as to the nature of the experiment and happy to proceed. Depending on the medical condition of the subject, it may be necessary to monitor them closely during the scanning, and communication is important so that the subject does not feel isolated.
[1] Purcell, E. M., Torrey, H. C. and Pound,
R. V. (1946) Resonance Absorption by Nuclear Magnetic Moments in a Solid.
Phys. Rev. 69,37-38.
[2] Bloch, F., Hansen, W. W. and
Packard, M. (1946) Nuclear
Induction. Phys. Rev. 69,127.
[3] Lauterbur, P. C. (1973) Image
Formation by Induced Local Interactions: Examples Employing Nuclear
Magnetic Resonance. Nature 242,190-191.
[4] Mansfield, P. and Grannell,
P. K. (1973) NMR `diffraction' in solids? J. Phys. C 6,
L422-L426.
[5] Abragam, A. (1961) `Principles of
Nuclear Magnetism'. Clarendon Press, Oxford.
[6] Callaghan, P. T. (1991) `Principles
of Nuclear Magnetic Resonance Microscopy', Clarendon Press,
Oxford.
[7] Stern, O. and Gerlach, W. (1924)
Uber die Richtungsquantelung im Magnetfeld. Ann. Phys. Leipzig.
74,673.
[8] Ljunggren, S. (1983) A Simple
Graphical Representation of Fourier-Based Imaging
Methods. J. Magn. Reson. 54,338-343.
[9] Locher, P. R. (1980) Computer
Simulation of Selective Excitation in NMR
Imaging. Phil. Trans. R. Soc. Lond .B 289,537-542.
[10] Morris, P. G., McIntyre,
D. J. O. and Rourke, D. E. (1989) Rational Approaches to the Design of
NMR Selective Pulses. NMR in Biomed. 2,257-266.
[11] Mansfield, P. (1988) Imaging by
Nuclear Magnetic Resonance. J. Phys. E: Sci. Instrum.
21,18-30.
[12] Damadian, R., Goldsmith, M. and
Minkoff, L. (1977) FONAR Image of the Live Human
Body. Physiol. Chem. & Phys. 9,97-100.
[13] Hounsfield, G. N. (1973)
Computerized Transverse Axial Scanning
(Tomography). Br. J. Radiol. 46,1016-1022.
[14] Edelstein, W. A., Hutchison,
J. M. S., Johnson, G. and Redpath, T. (1980) Spin warp NMR Imaging and
Applications to Human Whole-Body Imaging. Phys. Med. Biol.
25,751-756.
[15] Kumar, A., Welti, D. and Ernst,
R. R. (1975) NMR Fourier Zeugmatography. J. Magn. Reson.
18,69-83.
[16] Ernst, R. R. and Anderson,
W. A. (1966) Application of Fourier Transform Spectroscopy to Magnetic
Resonance. Rev. Sci. Instr. 37,93-102.
[17] Haase, A., Frahm, J., Matthaei,
D., Hänicke, W. and Merboldt, K.-D. (1986) FLASH Imaging. Rapid
NMR Imaging Using Low Flip-Angle Pulses. J. Magn. Reson.
67,258-266.
[18] Mansfield, P. (1977)
Multi-Planar Image Formation using NMR Spin Echoes. J. Phys. C
10,L55-L58.
[19] Mansfield, P. and Pykett,
I. L. (1978) Biological and Medical Imaging by
NMR. J. Magn. Reson. 29,355-373.
[20] Johnson, G., Hutchison,
J. M. S., Redpath, T. W. and Eastwood, L. M. (1983) Improvements in
Performance Time for Simultaneous Three-Dimensional NMR
Imaging. J. Magn. Reson. 54,374-384.
[21] Mansfield, P., Howseman, A. M.,
and Ordidge, R. J. (1989) Volumar Imaging using NMR Spin Echoes:
Echo-Volumar Imaging (EVI) at 0.1 T. J. Phys. E: Sci. Instrum.
22,324-330.
[22] Maudsley, A. A., Hilal, S. K.,
Perman, W. H. and Simon, H. E. (1983) Spatially Resolved High
Resolution Spectroscopy by "Four-Dimensional"
NMR. J. Magn. Reson. 51,147-152.
[23] Mansfield, P. (1988) Imaging by
Nuclear Magnetic Resonance. J. Phys. E: Sci. Instrum.
21,18-30.
[24] Kay, I. and Henkelman,
R. M. (1991) Practical Implementation and Optimisation of One-Shot
T1 Imaging. Magn. Reson. Med.
22,414-424.
[25] Gowland, P. and Mansfield,
P. (1993) Accurate Measurement of T1 in vivo in Less
Than 3 Seconds Using Echo-Planar
Imaging. Magn. Reson. Med. 30,351-354.
[26] Haase, A., Frahm, J.,
Hänicke, W. and Matthaei, D. (1985) 1H NMR Chemical
Shift Selective (CHESS) Imaging. Phys. Med. Biol.
30,341-344.
[27] Sumanaweera, T. S., Glover,
G. H., Binford, T. O. and Adler, J. R. (1993) MR Susceptibility
Misregistration Correction. I.E.E.E. Trans. Med. Imaging
12,251-259.
[28] Mansfield, P., Ordidge,
R. J. and Coxon, R. (1988) Zonally magnified EPI in real time by NMR.
J. Phys. E: Sci. Instrum. 21,275-280.
[29] Ehman, R. L. and Felmlee,
J. P. (1989) Adaptive Technique for High-Definition MR Imaging of
Moving Structures. Radiology 173,255-263.
[30] Howseman, A. M., Stehling,
M. K., Chapman, B., Coxon, R., Turner, R., Ordidge, R. J., Cawley,
M. G., Glover, P., Mansfield, P. and Coupland, R. E. (1988)
Improvements in Snap-Shot Nuclear Magnetic Resonance
Imaging. Br. J. Radiol. 61,822-828.
[31] Hayes, C. E., Edelstein, W. A.,
Schenck, J. F., Mueller, O. M. and Eash M. (1985) An Efficient, Highly
Homogeneous Radiofrequency Coil for Whole-Body NMR Imaging at 1.5
T. J. Magn. Reson. 63,622-628.
[32] Tenforde, T. S. (1979) `Magnetic
Field Effects on Biological Systems', Plenum Press, New York.
[33] Mansfield, P. and Morris,
P. G. (1982). `NMR Imaging in Biomedicine', in Advances in
Magnetic Resonance, Academic Press, New York.
[34] Cohen, M. S., Weisskoff, R. M.,
Rzedzian, R. R. and Kantor, H. L. (1990) Sensory Stimulation by
Time-Varying Fields. Magn. Reson. Med. 14,409-414.
[35] National Radiological Protection Board (1983) Revised Guidance on Acceptable Limits of Exposure during Nuclear Magnetic Resonance Clinical Imaging. Br. J. Radiol. 56, 974-977.