An MRI scanner is made up of four components: the magnet, gradient coils, r.f. transmitter and receiver, and the computer. In this section the general design and construction of these components is discussed. More specific details of the system used for the experiments in this thesis are given in the relevant chapters.
The magnet is the most expensive part of the whole scanner. The earliest systems were based around water-cooled resistive magnets, and for particular applications it is possible to use permanent magnets, but the majority of modern scanners use superconducting magnets. The reason for this is the high fields now desirable for MRI. Whole body resistive and permanent magnets are limited to around 0.3 T field strength, before their weight becomes prohibitively large. Superconducting magnets are able to generate much larger fields, and there are a number of 4.0 T whole body scanners now available. These magnets are constructed from materials such as NbTi alloy, which below a critical temperature of about 9 K loses its resistivity. Once started the current will flow in the coils indefinitely, provided that the temperature is kept below the critical temperature by cooling with liquid helium. The fields from such magnets are very stable with time, which is essential for an MRI system.
Of course one of the most important requirements for NMR is that the field is as homogeneous a possible, with tolerances as low as 1 p.p.m. required over the volume of interest. For this purpose, upon installation, the field is evened out as much as possible using ferromagnetic blocks placed inside the bore. As well as this, a set of resistive coils known as shim coils, are place within the bore of the magnet. These generate fields that vary with a particular function of position. Using these in combination it is possible to improve not only on the intrinsic homogeneity of the magnet, but also reduce the field effects due to susceptibility differences in the object being scanned.
The requirement of the gradient coils are twofold. First they are required to produce a linear variation in field along one direction, and secondly to have high efficiency, low inductance and low resistance, in order to minimise the current requirements and heat deposition.
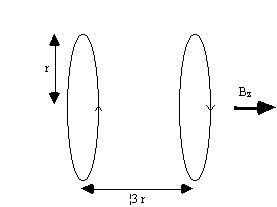
Linear variation in field along the direction of the field (traditionally labelled the z-axis) is usually produced by a Maxwell coil. This consists of a pair of coils separated by 1.73 times their radius as shown in Figure 2.30. Current flows in the opposite sense in the two coils, and produces a very linear gradient.
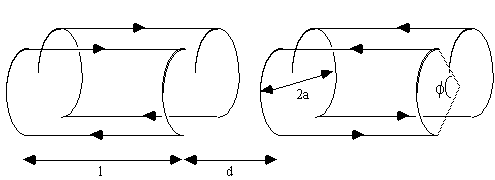
To produce a linear gradient in the other two axes requires wires running along the bore of the magnet. This is best done using a saddle-coil, such as the Golay coil shown in Figure 2.31. This consists of four saddles running along the bore of the magnet which produces a linear variation in Bz along the x or y axis, depending on the axial orientation. This configuration produces a very linear field at the central plane, but this linearity is lost rapidly away from this. In order to improve this, a number of pairs can be used which have different axial separations. If a gradient is required in an axis which is not along x,y or z, then this is achievable by sending currents in the appropriate proportions to Gx, Gy and Gz coils. If for example a transverse gradient G at an angle q to the x-axis is required, then a gradient Gcosq should be applied in the x direction, and Gsinq in y.
The magnitudes of the currents required, and the appropriate
waveforms are digitally generated, and converted into analogue
voltages. These are fed into power amplifiers which produce the
10's of amps required to generate the appropriate gradients. With
a technique such as EPI, the readout gradient is switched from
positive to negative at rates of anything up to 5kHz. This can be
made easier by employing resonant driving of the gradient coils. To
do this a large capacitor is placed in series with the coil, which
itself is an inductor. Such a circuit has a resonance at a frequency
of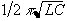 
, where L is the
inductance of the coil and C is the capacitance of the series
capacitor. When driving the coil at this frequency energy is
transferred between the capacitor and the inductor, thereby reducing
the load on the power amplifier.
The third main component of an MRI scanner is the r.f. coil. There are many different designs of coils, but they fall into two main categories; surface coils and volume coils.
As the name suggests, a surface coil rests on the surface of the object being imaged. In its simplest form it is a coil of wire with a capacitor in parallel. The inductance of the coil, and the capacitance form a resonant circuit which is tuned to have the same resonant frequency as the spins to be imaged. In practice, since the coil is connected to a power amplifier which will have an output impedance of 50W, and the coil will have an input impedance of the order of kilo-ohms, then on transmission a lot of the power will be reflected back. To overcome this, a second capacitor is added in series with the coil, as shown in Figure 2.32, so as to match the coil impedance to 50W.
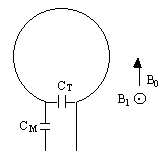
The homogeneous field produced by a simple surface coil like this is small, with the depth of penetration depending on the size of the coil. This however represents the main advantage of using a surface coil for imaging areas which lie close to the surface, as a good signal to noise ratio is achieved by inherently excluding noise signal from outside the region of interest. There are many designs of surface coil, and other localised coils for specific purposes. If however whole body images are required, or the regions of interest are far from the surface then a volume coil must be used.
Volume coils are large enough to fit either the whole body, or one specific region, such as the head or a limb, and have a homogeneous region which extends over a large area. The most commonly used design is a birdcage coil [31], as shown in Figure 2.33. This consists of a number of wires running along the z-direction, arranged to give a cosine current variation around the circumference of the coil.
The frequency supply is generated by an oscillator, which is modulated to form a shaped pulse by a double balanced mixer controlled by the waveform generator. This signal must be amplified to 1000's of watts. This can be done using either solid state electronics, valves or a combination of both.
It is possible to use the same coil to transmit and receive, or to use two separate coils. Either way it is necessary to gate the receiver side of the electronics. This is to prevent the excitation pulse, which is of the order of kilovolts, saturating or breaking the receiver electronics which are designed to detect signals of millivolts. This can again be done in a number of ways, but one such circuit for doing so is shown in Figure 2.34.
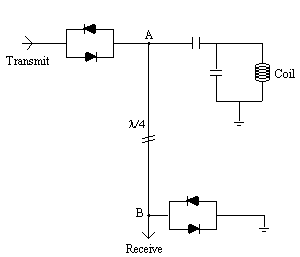
During the transmission pulse both sets of diodes will conduct, and the receiver is effectively shorted out. The short circuit at point B however looks like an open circuit at point A and so all the power is transmitted to the coil. The signal induced from the sample is too small to bias the diodes, and so is detected by the receiver circuitry.
The tiny e.m.f.'s from the sample are amplified at various stages and then mixed with a reference r.f. signal in a phase sensitive detector (p.s.d). Quadrature detection requires two p.s.d.'s, with a difference in phase of the reference signal of 90 degrees between them.
All the control of the scanner is handled by a computer. A schematic diagram of the whole system is shown in Figure 2.35.
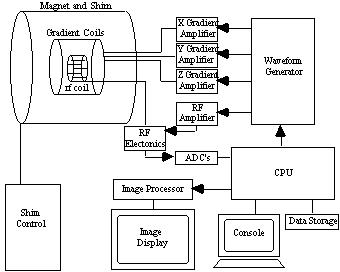
The scanning operation is controlled from a central computer. This specifies the shape of gradient and r.f. waveforms, and timings to be used, and passes this information to the waveform generator, which outputs the signals and passes them to be amplified and sent to the coils. The NMR signal, once it has been phase sensitively detected, is turned to a digital signal by an analogue to digital converter. The digital signal is then sent to an image processor for Fourier transformation and the image is displayed on a monitor.
The raw data, that is the signal before Fourier transformation, is stored to enable the application of corrections to the data in post processing. To allow the use of fast Fourier transformation, matrix sizes of 2n are usually used.