ONBI - Bayesian model fitting practical
Practical Overview
This practical requires Matlab. Go through the instructions and execute the listed commands in the Matlab command window (you can copy-paste). Raise your hand if you need help, but perhaps try first the "help" command in Matlab if you are unsure about Matlab syntax issues.
Contents:
- Linear models
- Learn basics of fitting linear models
- Sampling
- Learn to use Gibbs sampling for inference
- Nonlinear models
- Learn to fit a nonlinear model using 3 different methods
- Dynamic systems
- Learn to fit parameters to a dynamic system
Linear models
This practical will cover most of the examples that were discussed in the lecture, and you should be able to reproduce all the figures that were shown in the lecture.
We start with the simplest possible example of Bayesian inference. Imagine that we are measuring a certain quantity (e.g. temperature using a thermometer, actually let us say we ARE measuring temperature just for concreteness). We are going to assume that there exists a true unknown temperature, and that our measurement device is noisy. Therefore, we are going to make several measurements and we are going to use Bayesian inference.
We start by writing a generative model. Assuming we are measuring the temperature directly, the generative model can simply write:
y = a + noise;
In the above equation, y is the data, a
is a parameter of the model (the true unknown temperature), and the
noise is assumed to be additive.
We further need to make some distributional assumption on the noise. Most
commonly, the noise is assumed Gaussian with mean zero and standard
deviation s.
To complete the generative model, we need to set up a prior distribution on the parameter of the model. We will do this a little later.
Now generate some data using this generative model:
a = 5; % true mean (it's winter...) s = 4; % true noise std n = 4; % # data points y = a + s*randn(n,1); % Simulates fake data
Our generative model y=a+noise implies that the
likelihood function is given by:
p(y|a) = N(a,s^2)
Let us plot the data and the likelihood function as a function
of a.
va = linspace(-15,15,1000); N = length(va); lik = exp(-.5*sum((repmat(y,1,N)-repmat(va,n,1)).^2,1)/s^2); lik = lik/sum(lik); % normalise figure,hold on,grid on plot(y,0,'.','color','g','markersize',20); hli=plot(va,lik,'r','linewidth',2);
Make sure you understand the lines of code above. The use
of repmat is there to avoid writing loops. It is a
useful trick to have in your sleeve, but don't worry if you don't
understand it as it is not directly relevant for Bayesian inference.
You should be able to see that the likelihood function is a Gaussian centered around the data points (green dots). See what happens to the likelihood function when you change (i) the number of data points, (ii) the noise level, (iii) the true mean.
Now we turn to choosing a prior distribution on the temperature. We will use a Gaussian prior distribution (for simplicity) with zero mean and standard deviation 5 degrees:
a0 = 0; s0 = 5; pr = exp(-.5*(va-a0).^2./s0^2); pr = pr/sum(pr); hpr = plot(va,pr,'b','linewidth',2);
And finally we can write down the posterior distribution, which in this case is also a Gaussian (the product of two Gaussians is a Gaussian), where the mean/variance are given by combinations of the noise mean/variance and the prior mean/variance in what is referred to as "precision weighting":
beta = 1/s^2; % noise precision
beta0 = 1/s0^2; % prior precision
sp = 1/sqrt(n*beta+beta0); % posterior std
ap = (n*beta*mean(y)+beta0*a0)/(n*beta+beta0); % posterior mean
po = normpdf(va,ap,sp);
po = po/sum(po);
hpo=plot(va,po,'k','linewidth',2);
legend([hli hpr hpo],{'likelihood','prior','posterior'},'orientation','horizontal');
You should be able to see that the posterior distribution is close to the likelihood function. See how that might change depending on the set up (#data points, noise precision, prior precision).
Now we turn to linear regression. We will examine a very simple
model of the form y=a*x+noise, where a is
an unknown parameter, y is the data, and x
is a regressor (known). This regression model is very similar to the
linear model we just looked at, so we'll go through this very
quickly. Use the code below to generate some data and plot
likelihood/prior/posterior like before:
% Generate some data (you can play with changing mean, std, and #points)
a = 5; % true slope
s = 3; % true noise std
n = 20; % # data points
x = linspace(-1,1,n)'; % regressor
y = a*x + s*randn(n,1); % Simulates fake data
% plot likelihood
va=linspace(-15,15,100);N=length(va);
li = exp(-.5*sum((repmat(y,1,N)-x*va).^2,1)/s^2);
li = li/sum(li);
figure,
hold on
hli = plot(va,li,'r','linewidth',2);
% prior
a0 = 0;
s0 = 3;
pr = exp(-.5*(va-a0).^2./s0^2);
pr = pr/sum(pr);
hpr = plot(va,pr,'b','linewidth',2);
% posterior
beta = 1/s^2;
beta0 = 1/s0^2;
sp = 1/(beta0+beta*(x'*x));
ap = ( beta0*a0 + beta*x'*y ) / (beta0 + beta*(x'*x));
po = normpdf(va,ap,sp);
po = po/sum(po);
hpo = plot(va,po,'k','linewidth',2);
legend([hli hpr hpo],{'likelihood','prior','posterior'},'orientation','horizontal');
axis([-10 10 0 max(po)])
Now we will generate "samples" from the prior and the posterior distribution by generating random "slopes" that follow either prior or posterior distribution and plotting a line with the corresponding slope:
figure
axis([-1 1 -5 5])
plot(x,y,'k.','markersize',20); % draw data points
for i=1:20
samp = normrnd(a0,s0); % from prior
l1=line([-1 1],samp*[-1 1],'color','b','linestyle','--');
samp = normrnd(ap,sp); % from posterior
l2=line([-1 1],samp*[-1 1],'color','k');
end
legend([l1 l2],{'from prior','from posterior'},'orientation','horizontal');
You should be able to see that the posterior distribution has less spread than the prior.
Sampling
So far in our examples, we assumed that we knew the value of the noise variance. If we don't want to make that assumption, we can include the noise variance as an extra parameter in the model and infer on it using Bayes.
In this section, we consider such a model and we compare a grid search approach to Gibbs' sampling, i.e. getting samples from the posterior distribution. We are doing this because there is no analytical expression for the posterior distribution.
Consider a model of the form y=a*t+noise
where y is the data, t is some regressor
(e.g. time), and a an unknown parameter. Furthermore,
the noise is assumed to be N(0,s^2)
where s^2 is the unknown noise variance (we use the
square of s to denote the variance because it is always
positive. s is therefore the standard deviation).
Begin by generating some random data that obays this generative model:
a = 2; % true a sig = 5; % true sigma t = linspace(0,10,20)'; % regressor (known) % generate data y = a*t + sig*randn(size(t)); % plot data figure plot(t,y,'.','linewidth',2)
In order to complete the generative model, we need priors
on s^2 and a. We
choose p(s^2)=1/s^2 and p(a)=N(0,s0^2)
where s0 is very large (flat prior). In the lecture
we've shown these to be convenient for doing
Gibbs sampling:
Next we generate a grid for a and s^2, and
compute the posterior distribution at
each point on the grid.
% grid
va = linspace(0,5,100); % values of a
vs = linspace(.01,80,100); % values of s^2
posterior = zeros(length(vs),length(va));
for i=1:length(vs)
for j=1:length(va)
S = va(j)*t; % prediction
li = vs(i).^(-n/2)*exp(-sum((y-S).^2)/2/vs(i)); % likelihood
pr = 1/vs(i) * normpdf(va(i),0,1000); % prior
posterior(i,j) = li*pr; % posterior
end
end
posterior = posterior / sum(posterior(:));
Now we can have a look at the (joint) posterior distribution:
figure
imagesc(va,vs,posterior);
xlabel('a');
ylabel('s^2')
Now let us do the Gibbs sampling. This consists of drawing samples from the conditional posterior distribution of each parameter, where the conditioning is done over the current samples.
% gibbs sampling
niter = 10000; % number of iterations
a_s=zeros(niter,1); % container for samples for a
v_s=zeros(niter,1); % container for samples for s^2
% initial samples (you can change this to the maximum likelihood):
a_s(1)=2;
v_s(1)=10;
for i=2:niter
% samples a (Gaussian)
a_s(i) = normrnd(sum(t.*y)./sum(t.*t),sqrt(v(i-1)/sum(t.*t)));
% sample sig^2 (inverse-Gamma)
v_s(i) = 1/gamrnd( n/2, 2/sum( (y-a(i-1)*t).^2 ) );
end
Now plot both the grid solution and the samples
figure
imagesc(va,vs,posterior);
xlabel('a');
ylabel('s^2');
hold on
plot(a_s(1:20:end),v_s(1:20:end),'.k') % plot every 20th sample
Finally, we can calculate the marginal distributions in both cases (samples and grid) and compare them:
% plot marginals figure subplot(1,2,1),hold on [n,x]=hist(a_s,va);n=n/sum(n); % histogram from samples bar(x,n,'r'); plot(va,sum(posterior,1)','linewidth',2); % sum one dimension of grid subplot(1,2,2),hold on [n,x]=hist(v_s,vs);n=n/sum(n); bar(x,n,'r'); plot(vs,sum(posterior,2),'linewidth',2);
Pretty convincing no? The grid approach is the "exact" approach assuming the parameters can be considered to be bounded (lie within a range). But the grid approach is not really feasible if you need to estimate more that 4-5 parameters...
Nonlinear models
With nonlinear models, the likelihood function is not a Gaussian anymore, and therefore we don't necessarily have a nice analytic posterior distribution.
In this section, you will be fitting a non-linear model using three different methods: (1) a grid search approach, (2) the Laplace approximation, which is analytic, and (3) a sampling approach called Metropolis Hastings, which is one of the most flexible approaches to Bayesian inference.
The nonlinear model you will be fitting is of the
form: y=a*exp(-b*t)+noise, where a
and b are the unknown parameters. For simplicity, we
will assume uniform priors on these parameters, such that the
posterior distribution is "equal" to the likelihood function. We
will further assume that we know the standard deviation of the noise
for the first two methods (for the third method, we will parametrise
the noise variance but integrate it out of the model - see below).
Let's start by generating some data under this model:
a = 10; % true a
b = 2; % true b
t = linspace(0,2,100)';
sig = 5; % noise standard deviation
% data
y = a*exp(-b*t) + sig*randn(size(t));
% plot the data
figure
plot(t,y,'linewidth',2)
title('y=a*exp(-b*t)','fontsize',14)
First, we do a grid search. Run the code below and make sure you understand it:
% %%%%%%%%% grid %%%%%%%%%
w1 = linspace(0,20,50);
w2 = linspace(0,10,50);
[vw1,vw2] = meshgrid(w1,w2);
n = length(y);
N = length(vw1(:));
Y = repmat(y,1,N);
S = repmat(vw1(:)',n,1).*exp(-t*vw2(:)');
mu = sum((Y-S).^2,1)'/2/sig^2;
li = exp(-mu);
li = li/sum(li(:));
li = reshape(li,size(vw1));
% plot grid
imagesc(w1,w2,li);
hold on
h=plot(a,b,'+','color','k','markersize',20,'linewidth',2);
xlabel('a','fontsize',14);
ylabel('b','fontsize',14);
ind = find(li==max(li(:)));
[i,j]=ind2sub(size(vw1),ind);
l=line([min(w1) max(w1)],[w2(i) w2(i)]);set(l,'color','w');
l=line([w1(j) w1(j)],[min(w2) max(w2)]);set(l,'color','w');
In the resulting figure, the colors indicate the values of the likelihood (which is also the posterior, since our prior assumptions are uniform distributions). The black cross is the true parameter values, and the white cross is centered around the maximum posterior.
Now let's compare this distribution to the Laplace approximation. We first need to define the Laplace "around" the maximum posterior point. Then the approximation is simply a Gaussian distribution centered on the maximum posterior, and where the covariance matrix is given by the inverse Hessian (see lecture notes).
% maximum likelihood solution (from grid search, which is cheating... normally you would use fminsearch or something like that...)
ind = find(li==max(li(:)));
mu =[vw1(ind) vw2(ind)];
% derivatives of a.exp(-bt)
f = mu(1)*exp(-mu(2)*t);
fa = exp(-mu(2)*t);
fb = -mu(1)*t.*exp(-mu(2)*t);
faa = 0;
fab = -t.*exp(-mu(2)*t);
fbb = mu(1)*t.^2.*exp(-mu(2)*t);
% Hessian
Haa = sum( 2*fa.^2 - 2*(y-f).*(-faa) );
Hab = sum( 2*fa.*fb - 2*(y-f).*(-fab) );
Hbb = sum( 2*fb.^2 - 2*(y-f).*(-fbb) );
% Covariance
S = inv([Haa Hab;Hab Hbb]/2/sig^2);
% calculate on same grid using analytic formula for multivariate normal
lap = mvnpdf([vw1(:) vw2(:)],mu,S);
lap = lap/sum(lap(:));
lap = reshape(lap,size(vw1));
% plot Laplace
imagesc(w1,w2,lap);
[i,j]=ind2sub(size(vw1),ind);
l=line([w1(j) w1(j)],[min(w2) max(w2)]);set(l,'color','w');
l=line([min(w1) max(w1)],[w2(i) w2(i)]);set(l,'color','w');
xlabel('a','fontsize',14);
ylabel('b','fontsize',14);
Compare this joint distribution to the grid search approach (which is the true posterior). The approximation isn't so bad, but it is clear that it is not quite capturing the entire shape (the true distribution has a slight rotation).
Now let us calculate and plot marginal distributions for a and b from the two approached and compare them:
% plot marginals
figure,
subplot(1,2,1),hold on
plot(w1,[sum(li,1)' sum(lap,1)']);
l=line([a a],[0 .2]);set(l,'color','k');
xlabel('a');
subplot(1,2,2),hold on
plot(w2,[sum(li,2) sum(lap,2)]);
l=line([b b],[0 .2]);set(l,'color','k');
xlabel('b')
Finally, we will use Metropolis Hastings (MH) sampling to draw samples from the posterior distribution on a and b. Start by downloading the function MH, and use it in the following code:
% define a forward model (here y=a*exp(-bx)) myfun=@(x,c)(x(1)*exp(-x(2)*c)); % estimate parameters x0=[8;1]; % you can get x0 using nonlinear opt c=t; samples=mh(y,x0,@(x)(myfun(x,c))); a_mh=samples(:,1); b_mh=samples(:,2); % plot samples figure subplot(1,2,1),plot(a_mh) subplot(1,2,2),plot(b_mh)
The two plots report samples from the marginal posterior distribution on a and b.
The next bit of code compares the three distributions (two that can be viewed on a grid and one that consists of samples)
%% plot samples on joint posterior
figure
subplot(1,2,1)
imagesc(w1,w2,lap);
xlabel('a','fontsize',14);
ylabel('b','fontsize',14);
hold on
plot(a_mh,b_mh,'.k')
subplot(1,2,2)
imagesc(w1,w2,li);
xlabel('a','fontsize',14);
ylabel('b','fontsize',14);
hold on
plot(a_mh,b_mh,'.k')
Dynamic systems
Now we turn to a different class of problems that arise very often in biological mathematics, that of solving dynamic systems. Sometimes, you may want to fit the parameters of a dynamic system to measurents. I.e. your forward model for the data is a system of differential equations. In this final exercise, we will use Bayes and Metropolis Hastings to fit the parameters of a dynamic system.
As an example, we will consider the following dynamic system, which is called the "FitzHugh-Nagumo neural spike" model. This model is a two-dimensional coupled nonlinear differential equations like so:
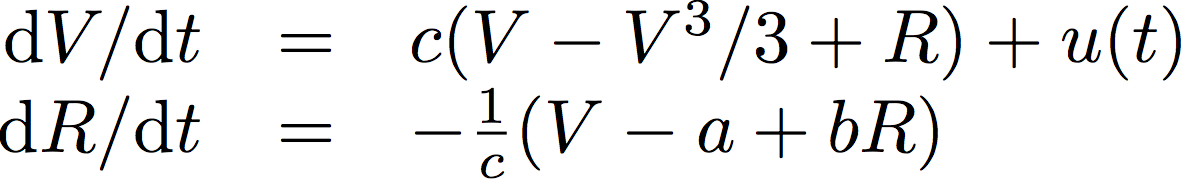
In the equations above, V is a voltage-like variable and R is a recovery variable. u(t) is the input, and a,b,c are free parameters. I like to have an intuition for how a dynamic system works and what to expect the solutions to look like, so here is my sort of interpretation:
The first equation is almost linear of the form dV/dt=V, which is an exponential growth. However, when V is too big, then the nonlinear term dominates (V^3) and brings the voltage back down. The second equation is linear (dR/dt=-R) which corresponds to an exponential decay-type dynamic, except that instead of decaying to zero, it decays to V (plus some constants), meaning that it is trying to decay towards the moving target that is V. So we should expect the system to oscillate (even without input u(t)) and the exact form of the oscillations will depend on the free parameters a,b and c.
Before we fit a,b,c, let us generate some data using this model and the ode functions in matlab. The following code does that by assigning some values to a,b,c and to the initial conditions. The input u(t) is a step function. In order to run the code below, first you need to download this matlab code, which the solver uses to generate the dynamic equations.
T = 50; % total duration in seconds
nt = 100; % number of time points to simulate
y0 = [0;0]; % initial condition (y is the vector [V;R])
% in the code below, I create a structure called 'opt'
% and then dump in this structure everything that the ODE
% solver will need to generate y(t)
opt.a = 0.1;
opt.b = 0.3;
opt.c = 2;
opt.u = zeros(nt,1); % input
opt.u(1:30)=5; % input is a step function
opt.tspan=[0 T]; % interval of the simulation
opt.tint=linspace(0,T,nt)'; % all time points
opt.y0=y0;
% here I change the tolerence of the ODE solver
% to make it faster
odeopt = odeset('AbsTol',1e-2,'RelTol',1e-2);
% solve the ODE (need to have the fhn function)
sol = ode45(@(t,x)(fhn(t,x,opt)),opt.tspan,opt.y0,odeopt);
Now let's plot the solution to the above system:
yout = deval(sol,opt.tint); % evaluate the solution
figure,
hold on
h1=plot(opt.tint(~~opt.u),0,'k.'); % plot the input u
h2=plot(opt.tint,yout,'.-'); % plot the solution
legend([h1(1);h2],{'input' 'V' 'R'})
It looks like the input drives the system variables to some sort of steady state values, but when the input is removed, the system oscillates, exactly as predicted by our intuition from above.
Now let us add some noise to this data:
y = yout + randn(size(yout)); figure plot(y','.')
Now, the purpose of the exercise here is to pretend that we have measured V and R (the noisy version), that we know the form of the dynamic system, and that we know the input u(t) as well as the initial conditions. What we don't know is the values of a,b,c. We are going to use our Metropolis Hastings sampling to sample from the posterior distribution on a,b and c.
First, we need a "Generative model" of the data, given a,b,c and initial conditions. Download this code and make sure you understand it (it is similar to the code you downloaded above)
Next, let's run the MCMC algorithm. We will also define starting values for a,b,c and lower/upper bounds so that the sampler doesn't get lost. In addition, we are not going to run it for very long, as it is rather slow. You should expect it to finish after about 90 second.
LB=[0.1 0.1 0.1]; % Lower bounds UB=[10 10 10]; % Upper bounds params.burnin=100; % #iterations before sampling starts params.njumps=1000; % #sampling iterations x0 = [0.2 0.2 3]; % initial 'guess' y = y'; % important so that y=[V;R] samples=mh(y(:),x0,@(x)(fhngen(x,opt)),LB,UB,params);
Now let's look at the samples and the predicted data.
% plotting samples plotmatrix(samples); % plotting data and predictions figure,hold on plot(y,'.'); pred=fhngen(mean(samples),opt); plot(reshape(pred,nt,2));
Well done. You have successfully fitted parameters of a dynamic system. You should know that the way we've done above with MCMC is rather slow, even with this few parameters (three). There is a lot of research (out of scope here) for how to do this more efficiently, particularly using the features of your dynamic systems (a little like when you used the Hessian of the likelihood function to do a Laplace approximation). But for now, this is all we have time for.
As a final exercise, can you add the initial conditions (y0) as an extra parameter to fit in the above system?
The End.
Created by Saad Jbabdi (saad@fmrib.ox.ac.uk)