Biomedical Sciences - Matlab introduction 3
Before you start
In this practical we are going to analyse some data using the MATLAB skills we have learned so far.
We are going to need some data. So first, please download this file: http://www.fmrib.ox.ac.uk/~saad/BMS/Titanic.xlsx onto the Desktop.
This is an Excel spreadsheet that contains some data on the passengers of the Titanic. You can find other cool datasets like this one at https://www.cooldatasets.com.
To view the data in Matlab, we are going to use a pretty neat MATLAB tool that deals with tables.
Open MATLAB and make sure to change the 'Current Folder' to the folder where you downloaded the data (Desktop).
Run the following command:
T = readtable('Titanic.xlsx');
The variable T is a table. Type T in the command line and then
type 'Enter' and you should see the different entries in the table.
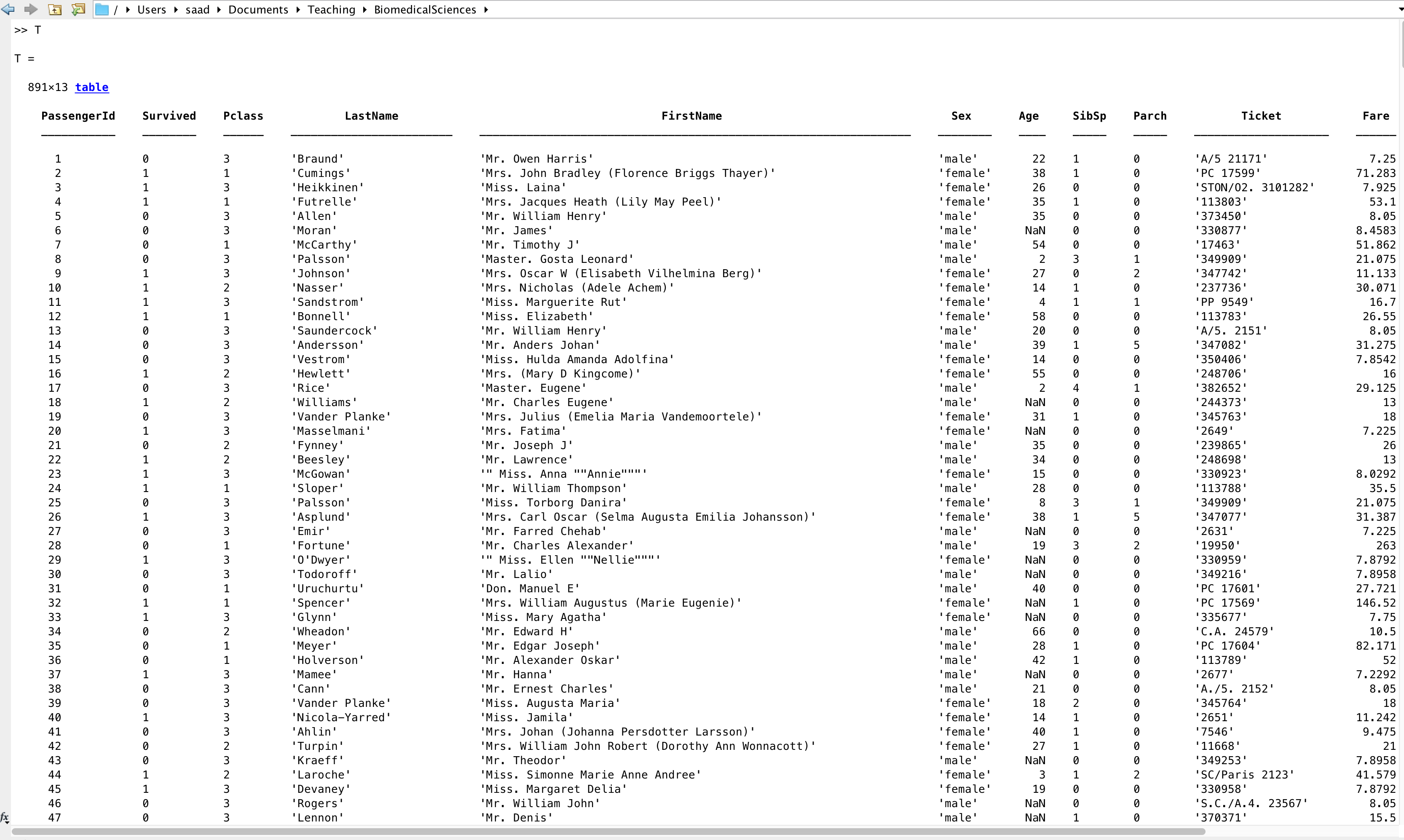
Each row is a different passenger, and each column is a passenger info. Here, we will concentrate on passenger 'Age', 'Sex', whether they have 'Survived', and their cabin class 'Pclass'. We will pretend that we are statisticians who were contacted by a newspaper at the time to report on the casualities of the terrible event.
Quick Stats
Q. How many passengers died?
For this we need the table entry
T.Survived:
NumPassengers = size(T,1);
NotDied = sum(T.Survived);
Died = NumPassengers - NotDied;
You should be able to see that there were 549 casualties. What proportion of passengers survived? Answer
Q. How many women/men were passengers?
For this one we need
the table entry T.Sex:
NumMen = sum(strcmp(T.Sex,'male'));
NumWomen = sum(strcmp(T.Sex,'female'));
In the commands above, we have used the MATLAB function
strcmp. This function compares the entries of the first
argument (here T.Sex) to the second argument ('male' or 'female')
and returns a vector of True/False (as binary 1 or 0). Thus the number of True in the top
command gives the number of men, and the number of True in the
second command gives the number of females.
Q. How many men/women died?
For this one we need to combine the entries T.Sex and
T.Survived. Think about it a little before you look up
the
answer.
Where has all this gallantry gone?
Well hang on, it looks bad for men but it could simply be that there were more men overall? We need to calculate the **proportion** of Men/Women that died or survived. Let's calculate the proportion that has survived:
PropMenSurvived = 1 - MenDied/NumMen
PropWomenSurvived = 1 - WomenDied/NumWomen
Can you see why it is 'one minus'? Answer
Basic visualisation
Now that we have calculated some basic numbers, let us plot some of the data to 'visualise' the numbers we just calculated.
Bar plots: Below we use a bar plot to visualise the number of men/women:
bar([NumMen NumWomen]);
set(gca, 'xticklabel', {'Men' 'Women'})
Another way to visualise this is by using the command
histogram, but for this we need to tell it that the
data in T.Sex is categorical (as opposed to numerical):
histogram(categorical(T.Sex))
It is easy to visually see that there are about twice as many men than there are women. Now we will use a bar plot again but separated by both gender and survival:
bar([NumMen-MenDied MenDied NumWomen-WomenDied WomenDied]);
set(gca, 'xticklabel', {'Men lived' 'Men died' 'Women lived' 'Women Died'})
As you can see, the discrepancy is visually striking.
Pie plots: Let's do one more type of plots: the pie
plot. It is useful for looking at proportions. We will plot three pie
plots in the same figure, and for this we will use subplot:
figure
subplot(1,3,1)
pie([NumMen NumWomen], {'Men' 'Women'})
subplot(1,3,2)
pie([NumMen-MenDied MenDied], {'Men lived' 'Men died'})
subplot(1,3,3)
pie([NumWomen-WomenDied WomenDied], {'Women lived' 'Women died'})
In case you are wondering, the way subplot works is you give it the number of rows and columns that constitute the grid of figures, and the third argument is the identifier of the current plot in the grid.
You like pie plots? Try the above using pie3
instead of pie for some 3D effect.
Further stats - Age
So far we have looked at 'categorical' data, which means that the values fall within discrete categories (e.g. True,False or male/female). Let us now look at some 'numerical' data. We will look at the age distribution of the passengers.
But before we start looking at the age distribution, we need to deal with an issue that occurs a lot in real world data: 'missing data'. If you look at the column for Age in the table, you will see that some entries say 'NaN'. This stands for 'Not A Number', and is simply a placeholder for empty entries (some passengers' ages were not recorded for some reason).
To deal with this here, we will simply create a copy of the table that does not contain NaNs by removing those passengers with missing age info from the table:
list_nonan = ~isnan(T.Age);
T = T(list_nonan,:);
Make sure you understand the command above, then move on. Our table no longer contains NaNs.
Before we carry on we need to update the number of passengers because we have removed those with missing age information:
NumPassengers = size(T,1);
Now, let's calculate the minimum, maximum, and average age. We will do this in two ways. First, we will use our knowledge of FOR loops and IF statements, then we will use MATLAB functions.
Let's start with the average:
average = 0;
for i=1:NumPassengers
average = average + T.Age(i);
end
average = average / NumPassengers;
Make sure you understand the code above. We begin by creating a variable called 'average', to which we add all the values of T.Age using the loop, and then we divide by the number of passengers at the end to get the average.
Let's now do the minimum and maximum:
minimum = +Inf;
maximum = -Inf;
for i=1:NumPassengers
if( T.Age(i) < minimum )
minimum = T.Age(i);
end
if( T.Age(i) > maximum )
maximum = T.Age(i);
end
end
Make sure you understand the code above. Can you see why I start by setting minimum to +Inf and maximum to -Inf?
Now let us calculate the variance and the standard deviation using a LOOP.
Recall that the variance is equal to the mean squared difference to the average. We have already calculated the average above. Can you try to calculate the variance? Answer
In MATLAB, we don't actually have to use LOOPS for these calculations, we can use the following MATLAB functions (check that they give you the same answer as the LOOPS we wrote):
Average = mean(T.Age);
Minimum = min(T.Age);
Maximum = max(T.Age);
Variance = var(T.Age,1);
Q. What is the average age of the survivors? Answer
Now one thing that is useful to do with numerical data is to visualise a histogram:
histogram(T.Age)
Let's make it look better by adding axes labels:
xlabel('Age (in years)')
ylabel('Counts')
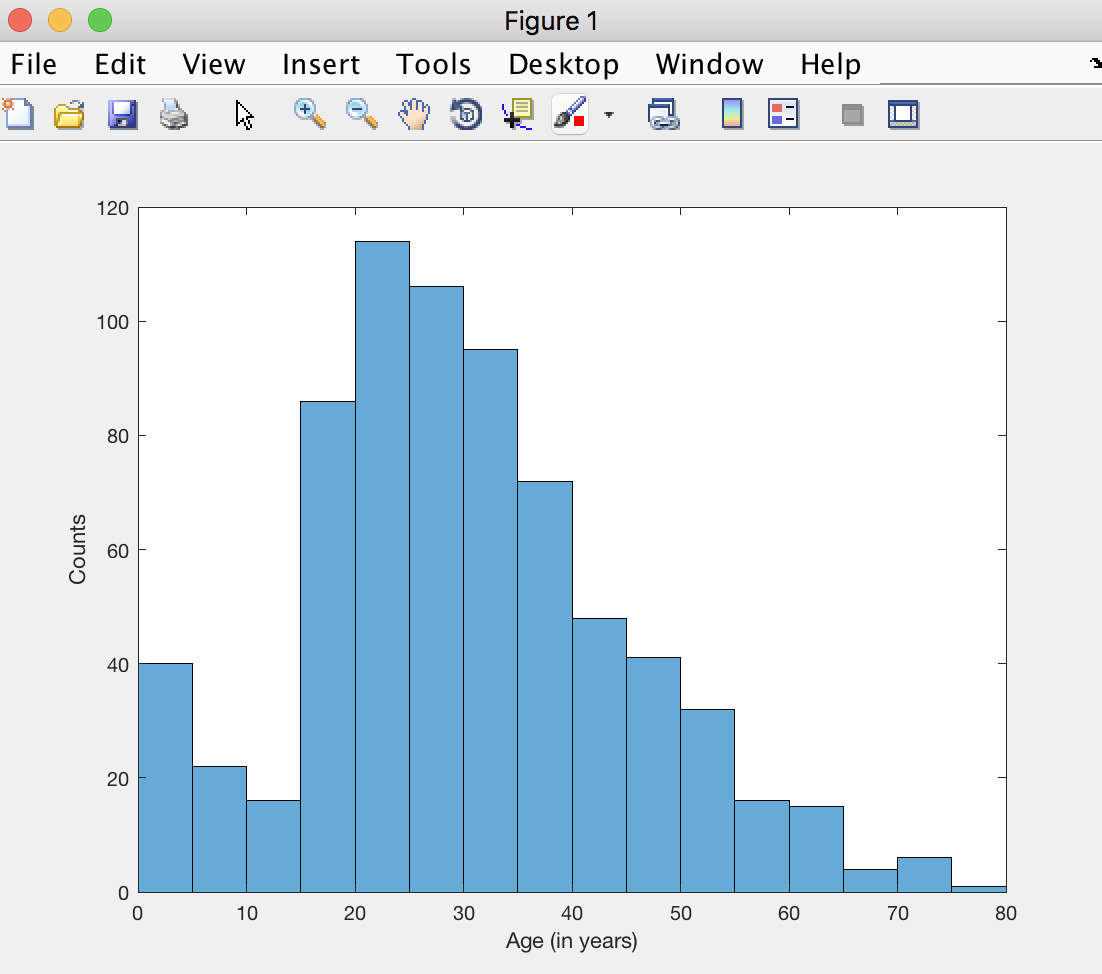
If you haven't encountered histograms before, these are just like the bar plots we have created earlier for counting the number of men and women, but here we are instead counting the number of people in each age range. For example, you should be able to see that around 40 passengers are kids younger than 5 years old, and that the maximum number of people is in the age range 20-25 years old.
One noticeable thing about this histogram is that it has some interesting 'structure': it is not just a simple bell-shaped curve. So perhaps calculating the mean survivor's age does not tell the full story. Let us look at the age histograms for survivors versus dead:
figure
histogram( T.Age( T.Survived == 1) );
hold on
histogram( T.Age( T.Survived == 0) );
legend({'Survived' 'Dead'})
This should produce a plot like this:
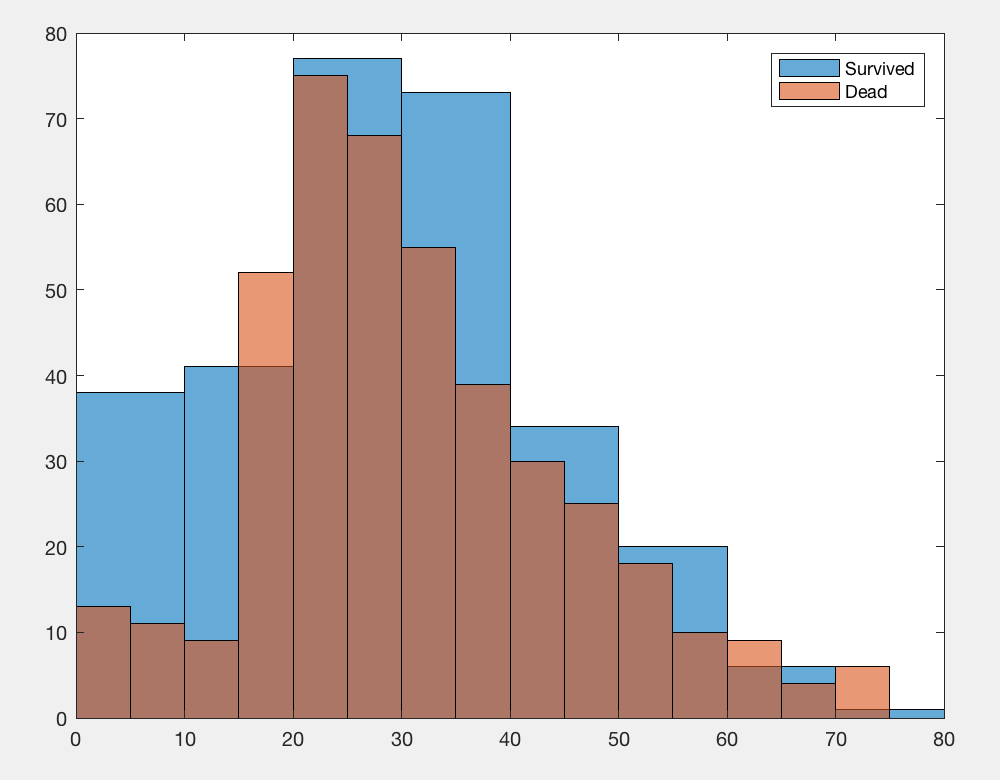
The two histograms are clearly different. For example, kids were much more likely to survive than adults. But is that true for both males and females? Let's plot the results separately for the two genders:
figure
histogram( T.Age( T.Survived == 1 & strcmp(T.Sex,'male')) );
hold on
histogram( T.Age( T.Survived == 0 & strcmp(T.Sex,'male')) );
legend({'Survived' 'Dead'})
title('Men')
figure
histogram( T.Age( T.Survived == 1 & strcmp(T.Sex,'female')) );
hold on
histogram( T.Age( T.Survived == 0 & strcmp(T.Sex,'female')) );
legend({'Survived' 'Dead'})
title('Women')
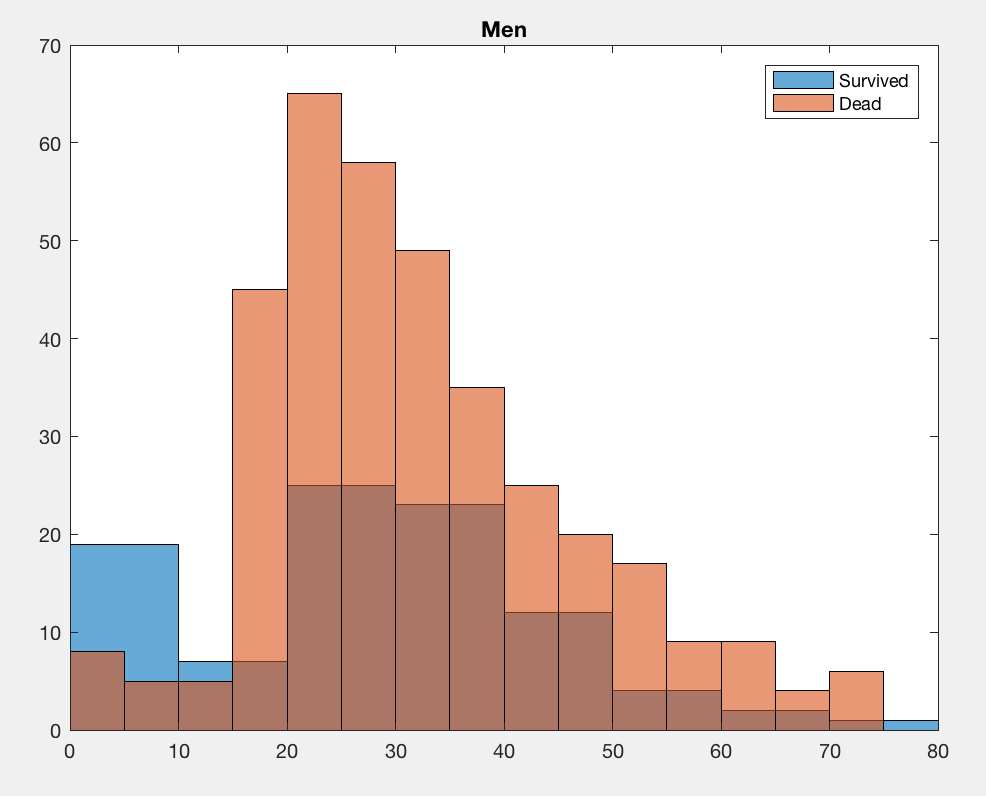
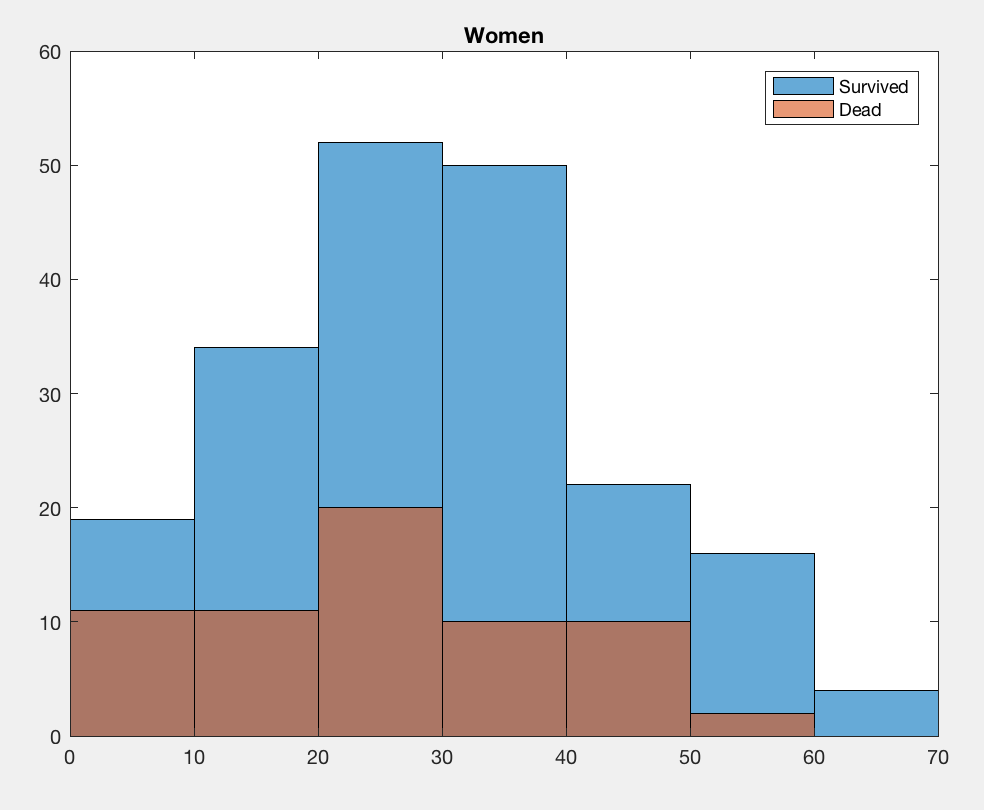
Now we see a massive difference. Kids who were boys were much more likely to survive than adult men, but for women the chances of survival were pretty balanced across all ages. If anything, adult women were a little more likely to survive than girls.
What we see here is an **interaction** effect. There is an interaction between age and gender when it comes to survival rates. There are statistical tools to quantify this interaction which we will not cover here. But instead, let us summarise the results in a table.
First let's create some vectors that index male/female, and kids/adults (we consider kids to be <12 years old and adults to be >20):
Males = strcmp( T.Sex, 'male');
Females = strcmp( T.Sex, 'female');
Kids = T.Age <= 12;
Adults = T.Age >= 20;
Now let's calculate survival rates for each group:
RateMaleKid = sum( T.Survived & Kids & Males ) / sum( Kids & Males )
RateFemaleKid = sum( T.Survived & Kids & Females ) / sum( Kids & Females )
RateMaleAdult = sum( T.Survived & Adults & Males ) / sum( Adults & Males )
RateFemaleAdult = sum( T.Survived & Adults & Females ) / sum( Adults & Females )
And display the results as a table:
stats = table([RateMaleKid RateFemaleKid; RateMaleAdult RateFemaleAdult]);
stats.Properties.RowNames = {'kids' 'adults'}
stats.Properties.VariableNames = {'male_vs_female'};
stats
Which should looke like:
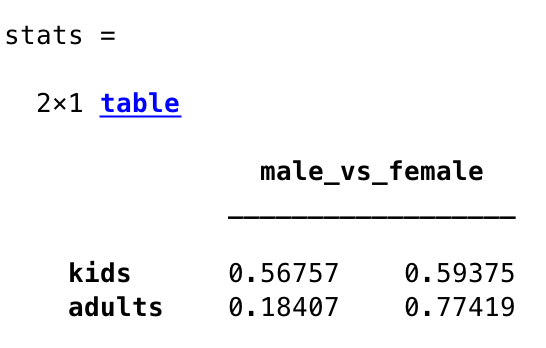
Now you should see clearly that kids were equally likely to survive regardless of their gender. You should also be able to see that it was clearly not a good idea to be an adult man on the Titanic.
Null Hypothesis testing
Let's finish by running a statistical test. We will test the hypothesis that first class passengers were more likely to survive than third class passengers.
For this, we will run a T-test (see your stats course for a
refresher). We will use the MATLAB built-in function
ttest2, which performs an unpaired T-test.
We begin by creating vectors for the subset of data that we need:
FirstClass = (T.Pclass == 1);
ThirdClass = (T.Pclass == 3);
Then we run the T-test:
[H,P] = ttest2( T.Survived(FirstClass), T.Survived(ThirdClass) )
You should be able to see that the output 'H' is equal to 1, which means that the null hypothesis that the two categories of passengers had the same number of survivors can be rejected with P<0.05. The second output is the actual P-value assosicated with the test, which is in fact much smaller than 0.05.
This test assumes the data is Gaussian-distributed. Is that the case here? Answer
If you have time, why not try to calculate more statistics on this dataset. Here are some example questions you may want to answer:
- Were First class passengers older or younger on average compared to Third class?
- Is the discrepancy between male and female death rates the same for First vs Third class passengers?
- What is the age of the captain?
The End.
Created by Saad Jbabdi (saad@fmrib.ox.ac.uk)