Biomedical Sciences - Matlab introduction 2

Before you start

Just like last time, start by opening MATLAB (the exact way to do this will depend on which type of computer you have, but generally if MATLAB is installed there should be an icon you can double-click on.

Today rather than typing commands in the command window, we will be using the MATLAB editor. This is a text editor where you can type all your matlab commands and programs, then MATLAB can run all the code written in there at once. It's also a useful way of keeping track of what you have done.

Here is a tip on how you can organise basic commands in an editor and execute them simply:

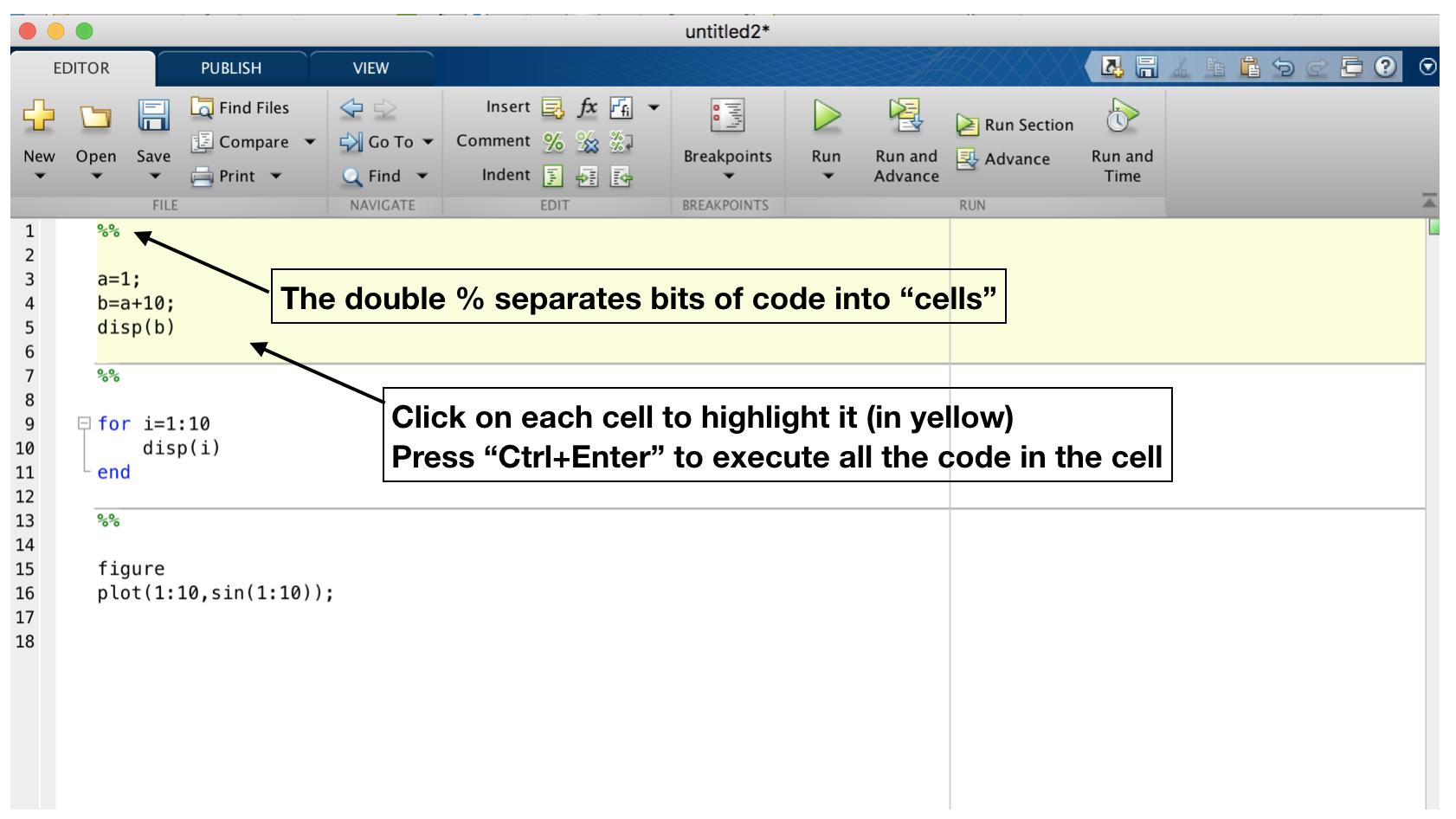
This practical is about FOR LOOPS and IF STATEMENTS.

What are 'FOR loops'?

FOR loops are useful in many circumstances. The purpose of a FOR loop is to 'repeat a set of instructions'. It is useful to have the ability to tell MATLAB to repeat an instruction without having to repeat the actual code.

For example, if we want MATLAB to do some operation 100 times, we could either write down the code for that operation 100 times in succession, or simply use a FOR loop and write the operation only once.

Let us do a simple example. The following command tells MATLAB to display a variable 10 times: 

      a=3;
      for i = 1:10
         disp(a);
      end

In the above, we first define a variable a to which we assign the value 3. Then we have a FOR loop that displays the variable a with the command disp. Let us examine the syntax of this FOR loop:

The FOR loop always begins begins with the word for and ends with the word end. Everything that is in between for and end gets executed.

Just after the word for, we have an iterator called i that will take values from 1 to 10. This means the FOR loop will run 10 times, each time the value of i will be incremented by 1, starting at 1 and ending at 10.

We can actually display the value of i inside the loop to check that is what is happening (also, the iterator doesn't need to be called i so let us use, say, j instead): 

     for j=1:10
        disp(j)
     end

Now what we have done so far are not very useful things to do with loops, they were just meant to introduce you to the syntax.

A more useful use of a FOR loop is to use the iterator to access a given entry of a variable. Let us do an example where we access entries in a cell array of words, e.g. calendar months. First define a variable with all the calendar months (remember: as in the intro to MATLAB 1, we use curly brackets for text): 

     months = {'January' 'February' 'March' 'April' 'May' 'June' 'July' 'August' 'September' 'October' 'November' 'December'};

Now we will use a FOR loop to extract the name of 'every other month' starting in January: 

    for i=1:2:12
       disp(months{i});
    end

Let us understand the syntax above. In the first line of the FOR loop, we have an iterator that starts at 1, ends at 12, with a step of 2. Then inside the loop, we use the iterator value to extract the relevant calendar month.

So to summarise FOR loops so far: we can use a FOR loop to repeat an operation. The iterator takes values during these repeats; and we can use the iterator inside the FOR loop to access elements of a variable.

Now let us perform actual mathematical operations inside FOR loops. A simple example is to write a FOR loop that calculates N! (factorial of N, or 1x2x3x4x...xN) for an integer number N.

First let us assign a value for N, for example 10: 

    N=10;

Now we will write a for loop that calculates N!. For that, we first define a variable F and assign it the value 1, then we use a loop: 

    F=1;
    for i=2:N
       F = F*i;
    end
    disp(F)

Notice our iterator starts at 2 and ends at N, and in each iteration we multiply the current value of F with i, and assign that result to the variable F. Try to do this sequentially (without the FOR loop) to understand what is going on.

Try with different values for N. You should see that the result grows very quickly as N gets bigger and bigger.

Let's do another example where we do some mathematical operations inside the FOR loop. Imagine we have two vectors a and b, and we want to calculate their 'scalar product' (a.k.a. 'dot product'). This means we multiply every element in a with the corresponding element in b, then sum the results. Let's first define two vectors (you can change this to whatever other values you like): 

    a=[0 1 4 3 0.1];
    b=[1 6 10 3 7];

A FOR loop that calculates the scalar product may look something like: 

    s=0;
    for i=1:length(a)
       s = s+a(i)*b(i);
    end
    disp(s);

Notice the use of the command length(a) to get the number of elements of a so that we know when to stop the loop.

What happens if a and b don't have the same length?

Why did we set s to zero before the start of the loop?

In matlab, calculating the scalar product of two vectors can be done in a number of different ways, for example, the two examples below use a different syntax that does not require a loop: 

    s=sum(a.*b);
    s=dot(a,b);

Double FOR loop: now let us have a look at FOR loops inside FOR loops! Remember in the intro to MATLAB plotting practical we drew the 2D function f(x,y)=sin(x2+y2). If you recall we did the following: 

    x=linspace(-2*pi/5,2*pi/5,100);
    y=linspace(-2*pi/5,2*pi/5,100);
    [x,y]=meshgrid(x,y);
    z=sin(x.^2+y.^2);

Now the use of meshgrid was to make sure that z calculates all possible combinations of x and y. We can achieve the same thing with a loop inside a loop as follows:

First, redefine x and y as vectors: 

    x=linspace(-2*pi/5,2*pi/5,100);
    y=linspace(-2*pi/5,2*pi/5,100);

Now we can use a double loop to get all combinations of x's and y's: 

    z = zeros(100,100);
    for i=1:100
       for j=1:100
          z(i,j)=sin( x(i)^2 + y(j)^2 );
       end
    end

How does it work? The first loop creates an iterator called i that increments its value by 1 every iteration. Inside each iteration on i, the second FOR loop creates a second iterator j that also takes values from 1 to 100.

Because the second loop is inside the first loop, each value of i is used in combination with every value of j.

Note that we initialise z to be a 100x100 table of zeros. Then for each row i, and for each column j, we extract the i-th element of x and j-th element of y to calculate z(i,j). This ensures that z contains combinations of all x's and all y's. You should be able to see that the two approaches yield identical results.

IF Statements

A useful thing to be able to do when programming is to ask a question with YES/NO answer and do something that depends on what the answer is. For example, inside a FOR loop, only execute a command if some statement is true, or exit the loop immediately if some statement is true.

Let's go back to the example we have seen above where we printed the name of every other calendar month. First define a variable with month names again (in case you've deleted it from the workspace): 

     months = {'January' 'February' 'March' 'April' 'May' 'June' 'July' 'August' 'September' 'October' 'November' 'December'};

Now we will create a loop that only displays the name of every other month, but where the iterator actually goes through all the number from 1 to 12 (rather than skip every other number). We include an IF statement that asks whether the iterator is even or odd: 

    for i=1:12
       if(rem(i,2)==1)
          disp(months{i});
       end  
    end

Let's try to understand the above commands. Firstly, we have an IF statement that ends with an end (just like the FOR loop does). Inside the brackets, we ask the question. In this particular case, we ask whether the iterator i is even or odd. We do this using the command rem. What does this do?

The command rem(x,y) gives the remainder of dividing x by y (see help rem). Therefore, when we write rem(i,2), we calculate the remainder of dividing i by 2. If you remember your high school maths, this should be equal to 0 for even numbers and to 1 for odd numbers.

So anything inside the IF statement will be executed if rem(i,2) is equal to 1, or else the FOR loop carries on.

You can also have an alternative command you can run if the statement inside the IF is false. This can be done with the commands if...else...end.

Let's do a fun example by finding which months have an "R" in them: 

   for i=1:12
       if( strfind(months{i},'r'))
          disp([months{i}  ' has an r in it.']);
       else
          disp([months{i}  ' does not have an r in it.']);
       end  
    end

The command strcmp(a,b) returns 'true' if the text 'b' is contained in 'a', and it returns 'false' otherwise. Note also the use of the square brackets [] to concatenate pieces of text together.

Excellent, now you know what a FOR loop is, and you know how to use an IF statement inside a FOR loop. Let us use these two pieces of knowledge to do something more complicated.

Something more complicated

Here we use FOR loops and IF statements to model the growth of a population of cells. We will consider a model where we start with a given number of cells, we know the birth-rate and the death-rate, and we try to see what happens to the number of cells over time.

To add IF statements, we will consider a rather biologically suspicious variation on the model. But first, let us play with the simple birth/death rate model.

We begin by creating a variable n0 (starting number of cells), and two rate variables b and d (respectively birth and death rates). We set these to some arbitrary values: 

    n0=100;
    b=0.01;
    d=0.05;

Now we write a loop that calculates the number of cells over time. Say at time t=1h, the number of cells is n0, and we simulate until t=5000h: 

    n=zeros(1,5000);
    for t=1:5000
       if(t==1);
         n(t)=n0;
       else
         n(t)=n(t-1)+b*n(t-1)-d*n(t-1);
       end
    end

Why did we need to treat the case t=1 separately?

Now let us plot the results: 

    plot(n)

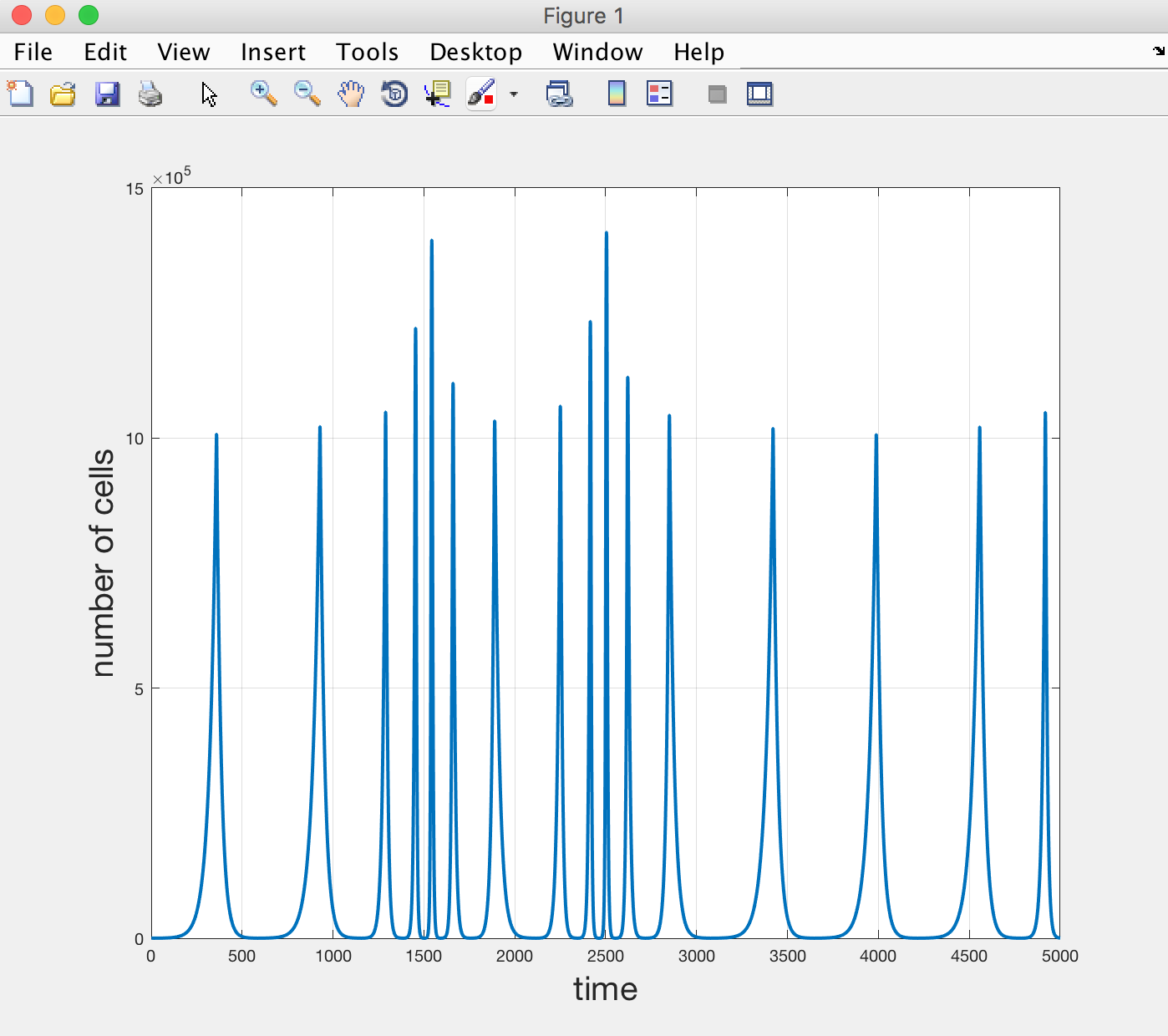
It is clear that the number of cells dies out exponentially (because the death rate is larger than the birth rate).

Now we add two new rules:

Although these rules sound arbitrary, we can still add them to our little matlab loop and see what happens: 

    n=zeros(1,5000);
    for t=1:5000
       if(t==1);
         n(t)=n0;
       else
         n(t)=n(t-1)+b*n(t-1)-d*n(t-1);
       end
       if(n(t)>1e6); d=2*d; b=b/2; end
       if(n(t)<1e2); d=d/2; b=b*2; end
    end

If you plot the results, you should be able to see a funky dynamic to the cell number, a bit aperiodic like so:

Something even more complicated

Now we are going to try to solve an actual problem using FOR loops and IF statements.

The problem is the following: 

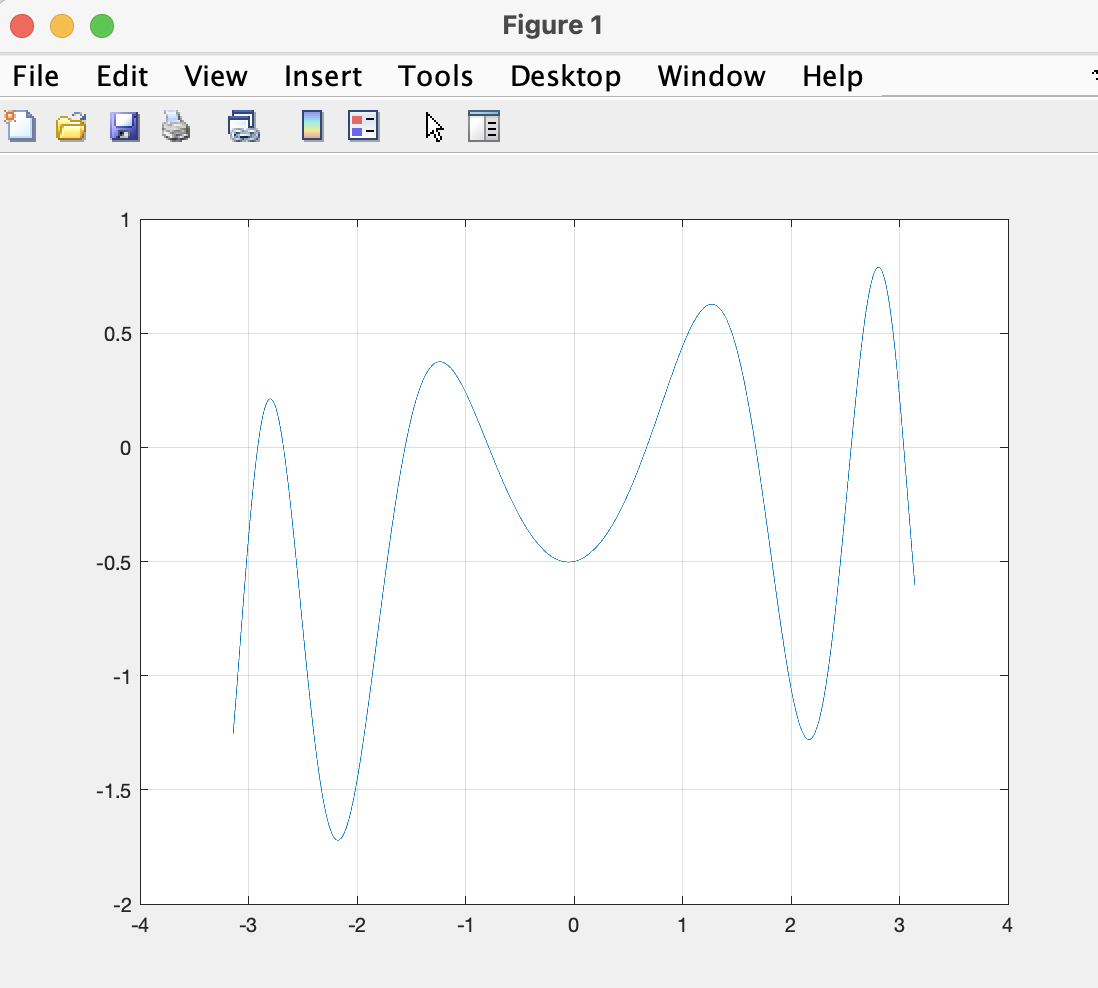
     Find the values of x between -π and π where sin(x2)+tan(x/10) is zero

If we plot this function you can see that it crosses zero a few times: 

    x=linspace(-pi,pi,10000);
    y=sin(x.^2)+tan(x/10);
    plot(x,y)
    grid on

Now let's try to solve the problem. If you are feeling brave you can stop reading now and try to solve it yourself.

First we define a vector x like we did above for plotting: 

    x=linspace(-pi,pi,10000);

Then we write a loop over the values of x, where we calculate the value of the function f(x)=sin(x2)+tan(x/10) and check whether f(x) changed from a positive to a negative value or vice versa. If it has done so, then it must have passed through zero (unless the function jiggles about very rapidly, which it doesn't): 

    v=[];
    for i=2:length(x)
       y1 = sin(x(i-1)^2)+tan(x(i-1)/10);
       y2 = sin(x(i)^2)+tan(x(i)/10);
       if( sign(y1*y2)<0 )
          z=(x(i-1)+x(i))/2;
          v=[v z];
       end
    end

Well, that is a lot of new commands! Let's start from the top:

We started with v=[]. This vector is going to store the values of x for which f(x) is zero. But it starts as an empty vector that we are going to fill as we go along in the loop.

Then we loop, starting at i=2 (can you see why?)

We calculate the value of f(x) at the current and previous position.

We calculate the sign of their product. This sign will only be negative if one of them is negative and the other positive (doesn't matter which). This means we have crossed zero!

We then calculate the value of x for which the crossing happens (we call it z). We approximate this with the middle point between the current and previous x position. This is an approximation of course, and can get better if x has a much higher 'resolution'.

We append this value z to the vector v and carry on till the end of the loop.

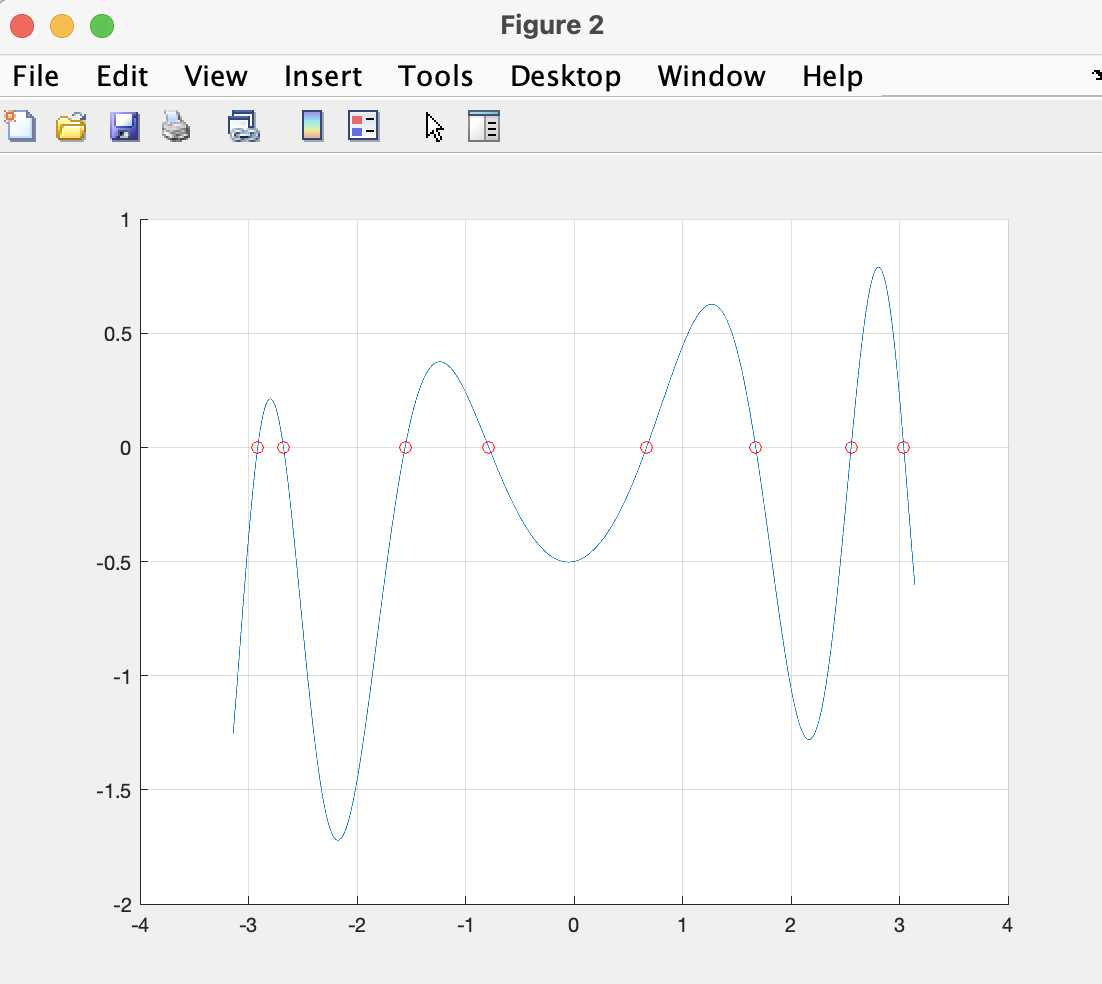
Now let's plot the function and the values at which it crosses zero: 

    figure,hold on
    plot(x,y);
    plot(v,0,'ro');
    grid on

You should be able to see this:

Final note: MATLAB programming can be very elegant. The examples above are meant to illustrate the use of FOR loops and IF statements, but these loops are not always necessary to solve these types of problems. For example, this last problem of finding zero crossings can be solved with this two-liner: 

     y = sin(x.^2)+tan(x/10);
     v = x(abs(diff(sign(y)))==2);

The End.

Created by Saad Jbabdi (saad@fmrib.ox.ac.uk)